Trong tất cả các hình nón nội tiếp trong hình cầu có thể tích bằng $\L

Trong tất cả các hình nón nội tiếp trong hình cầu có thể tích bằng $\Large 36\pi$, bán kính $\Large r$ của hình nón có diện tích xung quanh lớn nhất là

• A.

  A. $\Large r = \dfrac{3 \sqrt{2}}{2}$

• B.

  B. $\Large r = \dfrac{3}{2}$

• C.

  C. $\Large r = 2 \sqrt{2}$

• D.

  D. $\Large r = 3$

Chọn C

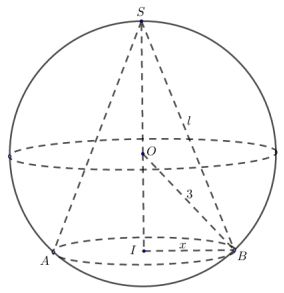
Vì hình cầu có thể tích là $\Large 36\pi$ nên bán kính hình cầu là $\Large R = 3$.

Ta có diện tích xung quanh của hình nón là $\Large S = \pi r l$.

Để hình nón có  diện tích xung quanh lớn nhất thì đỉnh của hình nón và đáy của hình nón phải ở hai phía so với đường tròn kính của hình cầu.

Đặt bán kính đáy hình nón là $\Large r = x$ với $\Large 0 < x \leq 3$

 và tâm của đáy hình nón là $\Large I$.

Ta có tam giác $\Large OIB$ vuông tại $\Large I$ nên $\Large OI = \sqrt{9 - x^{2}}$.

Chiều cao của hình nón là $\Large h = 3 + \sqrt{9 - x^{2}}$.

Độ dài đường sinh của hình nón là:

$\Large l = \sqrt{\left ( 3 + \sqrt{9 - x^{2}} \right )^{2} + x^{2}} = \sqrt{18 + 6\sqrt{9 - x^{2}}}$.

Suy ra diện tích xung quanh của hình nón là:

$\Large S = \pi x \sqrt{18 + 6\sqrt{9 - x^{2}}}$.

Đặt $\Large P = x \sqrt{18 + 6\sqrt{9 - x^{2}}}$ nên

$\Large P^{2} = x^{2} (18 + 6\sqrt{9 - x^{2}})$

và đặt $\Large \sqrt{9 - x^{2}} = t$, ($\Large 0 \leq t < 3$).

Khi đó:

$\Large P^{2} = (9 - t^{2})(18 + 6t)$ với $\Large 0 \leq t < 3$.

Xét hàm số $\Large y = (9 - t^{2})(18 + 6t)$

$\Large \Leftrightarrow y = -6t^{3} - 18t^{2} + 54t + 162$ có:

$\Large y{}' = -18t^{2} - 36t + 54 = 0$ 

$\Large \Leftrightarrow \left[\begin{array}{l}t=1 \\t=-3 (L) \\ \end{array}\right.$

Bảng biến thiên của hàm số  $\Large y = (9 - t^{2})(18 + 6t)$ với $\Large 0 \leq t < 3$:

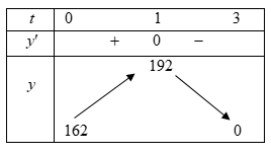
Từ bảng biến thiên,  $\Large P^{2}$ lớn nhất khi và chỉ khi $\Large t = 1$ suy ra $\Large P$ lớn nhất khi và chỉ khi $\Large t = 1$.

Khi đó $\Large S = \pi x \sqrt{18 + 6\sqrt{9 - x^{2}}}$ lớn nhất khi $\Large \sqrt{9 - x^{2}} = 1 \Leftrightarrow x = 2\sqrt{2}$ và diện tích xung quanh của mặt cầu khi đó là $\Large S = 8 \sqrt{3} \pi$.