Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình bình hành v

Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình bình hành và $\Large SA = SB = SC = 11$, góc $\Large \widehat{SAB} = 30^{o}$, góc $\Large \widehat{SBC} = 60^{o}$, góc $\Large \widehat{SCA} = 45^{o}$. Tính khoảng cách $\Large d$ giữa hai đường thẳng $\Large AB$ và $\Large SD$.

• A.

  A. $\Large 2 \sqrt{22}$

• B.

  B. $\Large \sqrt{22}$

• C.

  C. $\Large \dfrac{\sqrt{22}}{2}$

• D.

  D. $\Large 4 \sqrt{11}$

Chọn B

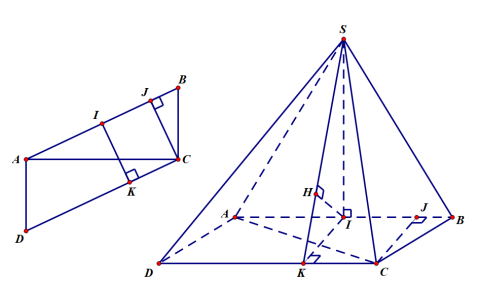
Trong tam giác $\Large \Delta SAB$ ta có $\Large SB^{2} = SA^{2} + AB^{2} - 2.SA.AB. \cos 30^{o}$ $\Large \Leftrightarrow AB = 11\sqrt{3}$.

Trong tam giác $\Large \Delta SBC$ ta có $\Large SB = SC = 11$, $\Large \widehat{SBC} = 60^{o}$ nên  $\Large \Delta SBC$ đều suy ra  $\Large BC = 11$.

Trong tam giác $\Large \Delta SCA$ ta có $\Large SC = SA = 11$, $\Large \widehat{SCA} = 45^{o}$ nên  $\Large \Delta SCA$ vuông cân tại $\Large S$ suy ra $\Large AC = 11\sqrt{2}$.

Xét tam giác $\Large \Delta ABC$ có $\Large BC^{2} + AC^{2} = AB^{2}$ do vậy $\Large  \Delta ABC$ vuông tại  $\Large C$.

Gọi $\Large I$ là hình chiếu của $\Large S$ lên mặt phẳng $\Large (ABCD)$ vì $\Large SA = SB = SC$ nên $\Large I$ là là tâm của đường tròn ngoại tiếp tam giác $\Large \Delta ABC$, vì $\Large \Delta ABC$ vuông tại $\Large C$ nên $\Large I$ là trung điểm của $\Large AB$ và $\Large SI \bot (ABCD)$

=> $\Large SI \bot CD$ (1). Vẽ $\Large IK \bot CD$ (2), $\Large IH \bot SK$ (3).

Từ (1) và (2) suy ra $\Large CD \bot (SIK)$ => $\Large CD \bot IH$ (4).

Từ (3) và (4) suy ra $\Large IH \bot (SCD)$ do đó khoảng cách $\Large d(I,(SCD)) = IH$.

Ta lại có $\Large AB // CD$ suy ra khoảng cách $\Large d(AB, SD) = d(AB,(SCD)) = d(I,(SCD)) = IH$.

Trong mặt phẳng đáy vẽ $\Large CJ \bot AB$ ta suy ra $\Large IK = CJ = \dfrac{CA.CB}{AB} = \dfrac{11\sqrt{6}}{3}$.

Trong tam giác $\Large SAB$ cân tại $\Large S$ có $\Large SI = \sqrt{SA^{2} - \dfrac{AB^{2}}{4}} = \dfrac{11}{2}$.

Trong tam giác $\Large SIK$ vuông tại $\Large I$ ta có $\Large IH = \dfrac{IK.SI}{\sqrt{IK^{2} + SI^{2}}} = \sqrt{22}$.