Giả sử tích phân $\Large I = \int_{1}^{5}\dfrac{1}{1 + \sqrt{3x + 1}}d

Giả sử tích phân $\Large I = \int_{1}^{5}\dfrac{1}{1 + \sqrt{3x + 1}}dx = a + b \ln 3 + c \ln 5$. Lúc đó:

• A.

  A. $\Large a + b + c = \dfrac{5}{3}$

• B.

  B. $\Large a + b + c = \dfrac{4}{3}$

• C.

  C. $\Large a + b + c = \dfrac{7}{3}$

• D.

  D. $\Large a + b + c = \dfrac{8}{3}$

Chọn B

Đặt $\Large t = \sqrt{3x + 1}$. Ta có:

$\Large t^{2} = 3x+ 1$

=> $\Large dx = \dfrac{2}{3}tdt$

Đổi cận

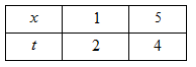
Ta có:

$\Large I = \int_{1}^{5}\dfrac{1}{1 + \sqrt{3x + 1}}dx$

$\Large I = \int_{1}^{4}\dfrac{1}{1+ t}.\dfrac{2}{3}. tdt$

$\Large I = \dfrac{2}{3} \int_{2}^{4}\dfrac{t}{t + 1}dt$

$\Large  I = \dfrac{2}{3} \int_{2}^{4}\left ( 1 - \dfrac{1}{t + 1} \right )dt$

$\Large I = \dfrac{2}{3} \left ( t - \ln \left | 1 + t \right | \right )|_{2}^{4}$

$\Large I = \dfrac{4}{3} + \dfrac{2}{3} \ln3 - \dfrac{2}{3} \ln5 $

Do đó: $\Large a = \dfrac{4}{3}$

$\Large b = \dfrac{2}{3}$

$\Large c = -\dfrac{2}{3}$

Vậy $\Large a + b + c = \dfrac{4}{3}$.