Trong mạch dao động LC lí tưởng đang có dao động điện từ tự do. Thời g

Trong mạch dao động LC lí tưởng đang có dao động điện từ tự do. Thời gian ngắn nhất giữa hai lần liên tiếp năng lượng từ trường bằng ba lần năng lượng điện trường là $10^{-4}$s. Thời gian giữa ba lần liên tiếp dòng điện trên mạch có giá trị lớn nhất là

• A. 3.$10^{-4}$s.
• B. 9.$10^{-4}$s.
• C. 6.$10^{-4}$s.
• D. 2.$10^{-4}$s.

Giải:  Thời gian giữa ba lần liên tiếp dòng điện trên mạch có giá trị cực đại chính là chu kì dao đông của mạch

${{E}_{}}=\frac{Q_{0}^{2}}{2C}{{\cos }^{2}}(\omega t+\phi )$.

${{E}_{t}}=\frac{Q_{0}^{2}}{2C}{{\sin }^{2}}(\omega t+\phi )$.

${{E}_{t}}=3{{E}_{d}}\Rightarrow {{\sin }^{2}}\left( \omega t+\varphi  \right)=3{{\cos }^{2}}\left( \omega t+\varphi  \right)$

$\Rightarrow 1-{{\cos }^{2}}\left( \omega t+\varphi  \right)=3{{\cos }^{2}}\left( \omega t+\varphi  \right)$

$\Rightarrow {{\cos }^{2}}\left( \omega t+\varphi  \right)=1/4\Rightarrow \cos \left( \omega t+\varphi  \right)=\pm 0,5$

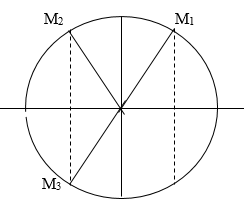
Trong một chu kì dao động khoảng thời gian giữa hai lần liên tiếp năng lượng từ trường bằng 3 lần năng lượng điện trường có hai khả năng:

$t_1$ = $t_{M1M2}$ = T/6  hoặc $t_2$  = $t_{M2M3}$  = T/3.

Bài ra cho thời gian ngắn nhất giữa hai lần liên tiếp $E_t$ = 3$E_d$  nên ta chọn $t_1$  = $10^{-4}$s 

=> chu kì T = 6.$10^{-4}$s => Chọn đáp án C