Trong không gian, cho tam giác ABC vuông tại A có AB = a và $\Large BC

Trong không gian, cho tam giác ABC vuông tại A có AB = a và $\Large BC = a\sqrt{5}$. Khi quay tam giác ABC quanh cạnh góc vuông AC ta được một khối tròn xoay. Thể tích của khối tròn xoay đó bằng

• A. A. $\Large \dfrac{2\pi a^{3}}{3}$
• B. B. $\Large \dfrac{4 \pi a^{3}}{3}$
• C. C. $\Large 4\pi a^{3}$
• D. D. $\Large 2\pi a^{3}$

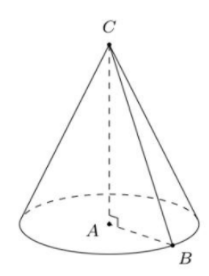
Khi quay tam giác ABC quanh cạnh góc vuông AC ta được một khối nón tròn xoay có bán kính đáy r = AB = a, chiều cao h = AC và độ dài đường sinh $\Large l = BC = a\sqrt{5}$

Ta có $\Large h = AC = \sqrt{BC^{2} - AB^{2}} = \sqrt{5a^{2}-a^{2}} = 2a$

Thể tích của khối nón là $\Large V = \dfrac{1}{3}\pi r^{2}h = \dfrac{1}{3}\pi a^{2}.2a = \dfrac{2\pi a^{3}}{3}.$