Trên mặt chất lỏng có hai nguồn $\Large S _{1} \text { và } S _{2}$ có

Trên mặt chất lỏng có hai nguồn $\Large S _{1} \text { và } S _{2}$ có phương trình lần lượt là $\Large u _{1}= u _{2}=4 \cos (40 \pi t )mm$, tốc độ truyền sóng là 120 cm/s. Gọi I là trung điểm của $\Large S _{1} S _{2}$. Hai điểm A, B nằm trên $\Large S _{1} S _{2}$ lần lượt cách I một khoảng 0,5 cm và 2 cm. Tại thời điểm t gia tốc của điểm A là $\Large 12 cm / s ^{2}$ thì gia tốc dao động tại điểm B có giá trị bằng

• A. $\Large -4 \sqrt{3} cm / s ^{2}$
• B. $\Large -12 cm / s ^{2}$
• C. $\Large 12 \sqrt{3} cm / s ^{2}$
• D. $\Large 4 \sqrt{3} cm / s ^{2}$

Phương pháp: 
Công thức tính bước sóng: $\Large \lambda=v T=\dfrac{v}{f}=\dfrac{v \cdot 2 \pi}{\omega}$
Xét pha dao động của hai phần tử A và B. 
Lời giải: 
Bước sóng: $\Large \lambda=v T=\dfrac{v}{f}=\dfrac{v \cdot 2 \pi}{\omega}=\dfrac{120.2 \pi}{40 \pi}=6 cm$
Biên độ dao động của hai phần tử A và B là: $\Large \left\{\begin{array}{l} A_{A}=\left|4 \cdot \cos \left(\dfrac{2 \pi}{6} \cdot 0,5\right)\right|=2 \sqrt{3} cm \\ A_{B}=\left|4 \cdot \cos \left(\dfrac{2 \pi}{6} \cdot 2\right)\right|=2 cm \end{array}\right.$

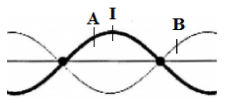
Ta thấy A và B là hai điểm thuộc hai bó sóng khác nhau, nên chúng dao động ngược pha, vì vậy ta có: 

$\Large \dfrac{a_{A}}{a_{B}}=\dfrac{-\omega^{2} u_{A}}{-\omega^{2} u_{B}}=-\dfrac{A_{A}}{A_{B}}=-\sqrt{3} \Rightarrow a_{B}=\dfrac{a_{A}}{-\sqrt{3}}=\dfrac{12}{-\sqrt{3}}=-4 \sqrt{3}\left( cm / s ^{2}\right)$

Chọn A.