Một con lắc lò xo treo thẳng đứng gồm quả cầu nhỏ có khối lượng m = 15

Một con lắc lò xo treo thẳng đứng gồm quả cầu nhỏ có khối lượng m = 150g và lò xo có độ cứng k = 60 N/m. Người ta đưa quả cầu đến vị trí lò xo không bị biến dạng rồi truyền cho nó một vận tốc ban đầu về $\Large v _{0}=\dfrac{\sqrt{3}}{2} m / s$ theo phương thẳng đứng hướng xuống. Sau khi được truyền vận tốc con lắc dao động điều hòa. Chọn thời điểm t = 0 là lúc quả cầu được truyền vận tốc, lấy $\Large g =10 m / s ^{2}$. Thời gian ngắn nhất tính từ lúc t = 0 đến lúc lực đàn hồi tác dụng lên vật có độ lớn 3 N là

• A.

  $\Large \dfrac{\pi}{5} s$

• B.

  $\Large \dfrac{\pi}{60} s$

• C.

  $\Large \dfrac{\pi}{20} s$

• D.

  $\Large \dfrac{\pi}{30} s$

Phương pháp: 
Tại vị trí cân bằng, lò xo dãn là $\Large \Delta l=\dfrac{m g}{k}$
Biểu thức tính tần số góc $\Large \omega=\sqrt{\dfrac{k}{m}}$
Áp dụng công thức độc lập với thời gian $\Large A^{2}=x^{2}+\dfrac{v^{2}}{\omega^{2}}$
Biểu thức độ lớn lực đàn hồi $\Large F=k \Delta$
Lời giải: 
Tại vị trí cân bằng lò xo dãn: $\Large \Delta l_{0}=\dfrac{m g}{k}=\dfrac{0,15 \cdot 10}{60}=0,025 m=2,5 cm$
Tần số góc: $\Large \omega=\sqrt{\dfrac{k}{m}}=20 rad / s$
Biên độ dao động: $\Large A^{2}=x^{2}+\dfrac{v^{2}}{\omega^{2}}=(-2,5)^{2}+\dfrac{\left(\dfrac{\sqrt{3}}{2} \cdot 100\right)^{2}}{20^{2}}=25 \Rightarrow A=5 cm$

Tại t = 0 tức là lúc truyền vận tốc thì lò xo không giãn: $\Large F_{d h}=0 N$
Khi lực đàn hồi là 3N thì: $\Large F=k \Delta \Rightarrow \Delta l=\dfrac{3}{60}=0,05 m =5 cm$
Ta có hình vẽ: 

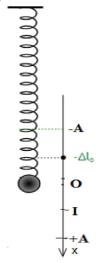
I là vị trí mà lò xo dãn 5cm, x = 2,5cm 
Thời gian t là: $\Large t=\dfrac{\arcsin \dfrac{2,5}{5}+\arcsin \dfrac{2,5}{5}}{2 \pi} \cdot T=\dfrac{T}{6}=\dfrac{2 \pi}{\omega .6}=\dfrac{2 \pi}{20.6}=\dfrac{\pi}{60} s$
Chọn B.