Xét một đoạn mạch xoay chiều mắc nối tiếp gồm cuộn dây D và tụ điện C.

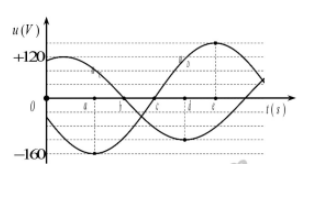
Xét một đoạn mạch xoay chiều mắc nối tiếp gồm cuộn dây D và tụ điện C. Điện áp tức thời ở hai đầu cuộn dây D và điện áp tức thời ở hai đầu tụ điện C được biểu diễn bởi các đồ thị $\Large u _{ D }$, như hình vẽ. Trên trục thời gian t, khoảng cách giữa các điểm a - b, b - c, c - d, d – e là đều nhau. Điện áp hiệu dụng ở hai đầu đoạn mạch gần bằng với giá trị nào nhất sau đây?

  

• A. 80 V
• B. 140 V
• C. 200 V
• D. 40 V

Phương pháp: 
Từ đồ thị ta thấy khoảng thời gian từ a đến e là $\Large \dfrac{T}{2}$
Mà khoảng cách a - b; b - c; c - d; d – e là đều nhau nên $\Large t_{a-b}=t_{b-c}=t_{c-d}=t_{d-e}=\dfrac{T}{8}$
Tại d ta thấy $\Large u_{C}=-U_{0 C}=120 V \Rightarrow$ tại e: $\Large u_{c}=-\dfrac{U_{0 C}}{\sqrt{2}}$
Tại e: $\Large \left\{\begin{array}{l} u_{D}=U_{0 D} \\ u_{C}=-\dfrac{U_{0 C}}{\sqrt{2}} \end{array}\right.$
Độ lệch pha giữa $\Large u_{D} \text { và } u_{C}$ là $\Large \dfrac{3 \pi}{4}$
Ta có $\Large \overrightarrow{ U _{0}}=\overrightarrow{U_{0 D}}+\overrightarrow{U_{0 C}}$
Lời giải: 
Từ đồ thị ta thấy khoảng thời gian từ a đến e là $\Large \dfrac{T}{2}$
Mà khoảng cách a - b; b - c; c- d; d - e là đều nhau nên $\Large t_{a-b}=t_{b-c}=t_{d-e}=\dfrac{T}{8}$
Tại d ta thấy $\Large u_{C}=-U_{0 C}=120 V \Rightarrow$ tại e: $\Large u_{C}=-\dfrac{U_{O C}}{\sqrt{2}}$
Tại e: $\Large \left\{\begin{array}{l} u_{D}=U_{0 D} \\ u_{C}=-\dfrac{U_{0 C}}{\sqrt{2}} \end{array}\right.$
Độ lệch pha giữa $\Large u_{D} \text { và } u_{C}$ là $\Large \dfrac{3 \pi}{4}$
Lại có $\Large \overrightarrow{U_{0}}=\overrightarrow{U_{0 D}}+\overrightarrow{U_{0 C}} \Rightarrow U_{0}^{2}=U_{0 D}^{2}+U_{0 C}^{2}+2 U_{0 D} \cdot U_{0 c} \cdot \cos \dfrac{3 \pi}{4}$

$\Large \Rightarrow U_{0}^{2}=160^{2}+120^{2}=2.160 .120 \cdot \cos \dfrac{3 \pi}{4}$$\Large \Rightarrow U_{0}=113,35 V \Rightarrow U=\dfrac{U_{0}}{\sqrt{2}}=80,147 V$

Chọn A.