Ở mặt nước có 2 nguồn sóng cơ A và B cách nhau 15 cm, dao động điều hò

Ở mặt nước có 2 nguồn sóng cơ A và B cách nhau 15 cm, dao động điều hòa cùng tần số,cùng pha theo phương vuông góc với mặt nước. Điểm M nằm trên AB, cách trung điểm O là 1,5cm, là điểm gần O nhất luôn dao động với biên độ cực đại.Trên đường tròn O, đường kính 20cm, nằm ở mặt nước có số điểm luôn dao động với biên độ cực đại là:

 

• A. A.18
• B. B.16
• C. C.32
• D. D.17

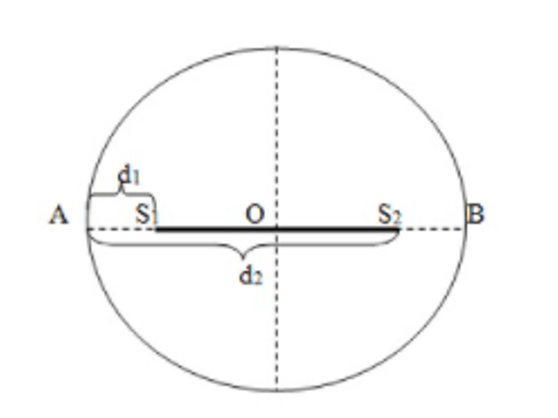
Sóng tại M có biên độ cực đại khi ${{d}_{2}}-{{d}_{1}}=k\lambda $

Ta có${{d}_{1}}=15/2+1,5=9cm;{{d}_{2}}=15/2-1,5=6cm$

Khi đó ${{d}_{2}}-{{d}_{1}}$=3.Với điểm M gần O nhất, chọn k=1. Khi đó ta có $\lambda =3$.Số điểm dao động cực đại trên AB là:

$-{{S}_{1}}{{S}_{2}}\le {{d}_{2}}-{{d}_{1}}\le {{S}_{1}}{{S}_{2}}$

Hay $-15\le k\lambda \le 15<=>-5\le k\le 5$

Vậy số điểm dao động với biên độ cực đại trên đường tròn tâm O bán kính 20cm là:

$n=10{{x}^{2}}-2=18$cực đại( ở đây tại A và B là 2 cực đại do đó chỉ có 8 đường cực đại cắt đường tròn tại 2 điểm, 2 cực đại là A và B tiếp xúc với đường tròn)