Trên mặt phẳng chất lỏng hai nguồn kết hợp A,B cách nhau 40 cm dao độn

Trên mặt phẳng chất lỏng hai nguồn kết hợp A,B cách nhau 40 cm dao động cùng pha. Biết sóng do mỗi câu nguồn phát ra có tần số f = 10 Hz vận tốc truyền sóng 2 m/s. Gọi M là điểm nằm trên đường vuông góc với AB tại đó A dao động với biên độ cực đại. Đoạn AM có giá trị lớn nhất là

• A. A.20 cm
• B. B.30 cm
• C. C.40 cm
• D. D.50 cm

Ta có $\lambda=v/f=200/10=20(cm)$

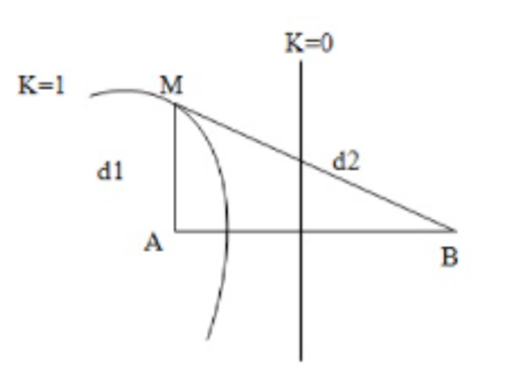
 M là một cực đại giao thoa nên đoạn AM có giá trị lớn nhất thì M phải nằm trên vân cực đại bậc 1 như hình vẽ và thỏa mãn ${{d}_{2}}-{{d}_{1}}=k\lambda =1.20=20(cm)(1)$(Do lấy k=+1)

 Mặt khác do tam giác AMB là tam giác vuông tại A nên ta có: $AM={{d}_{2}}=\sqrt{{{(AB)}^{2}}+{{(AM)}^{2}}}=\sqrt{{{40}^{2}}+{{d}_{1}}^{2}}$

Thay (2) vào (1) được:

$\sqrt{{{40}^{2}}+{{d}_{1}}^{2}-{{d}_{1}}}=20=>{{d}_{1}}=30(cm)$