Một vật dao động điều hòa dọc theo trục Ox, có đồ thị biểu diễn sự phụ

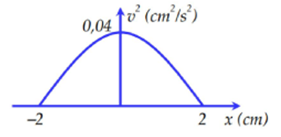
Một vật dao động điều hòa dọc theo trục Ox, có đồ thị biểu diễn sự phụ thuộc của bình phương vận tốc ($\large v_2$) vào li độ x như hình vẽ. Tần số góc của vật là 

• A. A. 10 rad/s
• B. B. 2 rad/s.
• C. C. 20 rad/s
• D. D. 40 rad/s.

Phương pháp: 
Phương trình của li độ và vận tốc: $\large \left\{ \begin{align} & x=A.cos\left( \omega t+\varphi  \right) \\ & v=-\omega A.\sin \left(\omega t+\varphi  \right) \\ \end{align} \right.$
Lời giải: 
Phương trình dao động điều hòa và phương trình vận tốc: 
$\large \left\{ \begin{align} & x=A.cos\left( \omega t+\varphi  \right) \\ & v=-\omega A.\sin \left( \omega t+\varphi  \right)\Rightarrow {{v}^{2}}={{\omega }^{2}}.{{A}^{2}}.{{\sin }^{2}}\left( \omega t+\varphi  \right) \\ \end{align} \right.\Rightarrow {{v}^{2}}={{\omega }^{2}}.\left( {{A}^{2}}-{{x}^{2}} \right)$

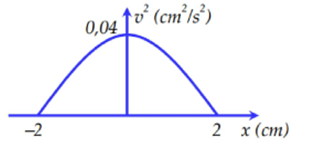
Từ đồ thị, ta thấy biên độ A = 2cm và tại $\large \left\{ \begin{align}& x=0 \\ & {{v}^{2}}=0,04 \\ \end{align} \right.$ 
Vậy ta có: $\large {{v}^{2}}={{\omega }^{2}}.{{A}^{2}}=0,04\Rightarrow \omega =\sqrt{\dfrac{{{v}^{2}}}{{{A}^{2}}}}=\sqrt{\dfrac{0,04}{0,{{02}^{2}}}}=10\left( rad/s \right)$ 
Chọn A.