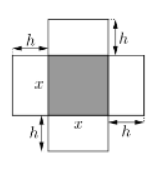
Một hộp không nắp được làm từ một mảnh cactong theo hình vẽ. Hộp có đá
Lưu về Facebook:
MỤC LỤC
Câu hỏi:
Một hộp không nắp được làm từ một mảnh cactong theo hình vẽ. Hộp có đáy là hình vuông cạnh x(cm), chiều cao là h(cm) và thể tích là 500cm3. Tính độ dài cạnh hình vuông x sao cho chiếc hộp làm ra tốn ít bìa cactong nhất.

Đáp án án đúng là: D
Lời giải chi tiết:
Thể tích khối hộp V=x.x.h=x2h=500⇒h=500x2
Để chiếc hộp làm ra ít tốn bìa cactong nhất khi và chỉ khi diện tích toàn phần của hộp là nhỏ nhất. Diện tích toàn phần của hộp (không nắp)
Stp=Sday+Sxungquanh=x.x+4hx=x2+4hx
=x2+4x⋅500x2=x2+2000x=x2+1000x+1000xcosi≥33√10002
Dấu "=" xảy ra ⇔x2=1000x=1000x⇔x3=1000⇔x=10
Đáp án D
Cách 2: Xét hàm f(x)=x2+2000x với x>0
Xem thêm các bài tiếp theo bên dưới