Một viên đá dạng khối chóp tứ diện đều và tất cả các cạnh đều bằng $\l
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Một viên đá dạng khối chóp tứ diện đều và tất cả các cạnh đều bằng $\large a$, người ta cưa viên đá theo mặt phẳng song song với mặt đáy của khối chóp để chia viên đá thành hai phần có thể tích bằng nhau. Tính diện tích thiết diện của viên đá bị cưa với mặt phẳng nói trên.
Đáp án án đúng là: A
Lời giải chi tiết:
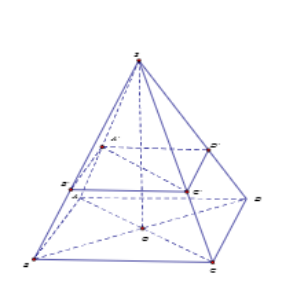
Từ giả thiết $\large\Rightarrow V_{S.A'B'C'D'}=\frac{1}{2}V_{S.ABCD}\Rightarrow V_{S.A'B'C'}=\frac{1}{2}V_{S.ABC}$ (do khối chóp tứ giác đều)
$\large\Rightarrow \frac{V_{S.A'B'C'}}{V_{S.ABC}}=\frac{1}{2}=\left (\frac{SA'}{SA} \right )^{3}\Rightarrow SA'=\frac{SA}{\sqrt[3]{2}}=\frac{a}{\sqrt[3]{2}}\Rightarrow A'B'=SA'=\frac{a}{\sqrt[3]{2}}\Rightarrow S_{td}=A'B'^{2}=\frac{a^{2}}{\sqrt[3]{4}}$
Đáp án D
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp $\large S.ABCD$ có đáy $\large ABCD$ là hình chữ nhật vớ
- Cho hình chóp $\large S.ABCD$ có đáy là hình vuông, gọi $\large M$ là
- Cho hình lập phương $\large ABCD.A'B'C'D'$ cạnh $\large a$. Tính góc t
- Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2. Gọi M, N
- Cho mặt cầu ( $\large S_{1}$ ) có bán kính $\large R_{1}$ , mặt cầu (