Cho hình chóp S.ABCDS.ABCD có đáy là hình vuông, gọi MM là

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCDS.ABCD có đáy là hình vuông, gọi MM là trung điểm của ABAB. Tam giác SABSAB cân tại SS và nằm trong mặt phẳng vuông góc với đáy (ABCD)(ABCD), biết SD=2a√5,SCSD=2a√5,SC tạo với đáy (ABCD)(ABCD) một góc 60∘60∘ . Tính theo aa khoảng cách hh giữa hai đường thẳng MDMD và SASA
Đáp án án đúng là: B
Lời giải chi tiết:
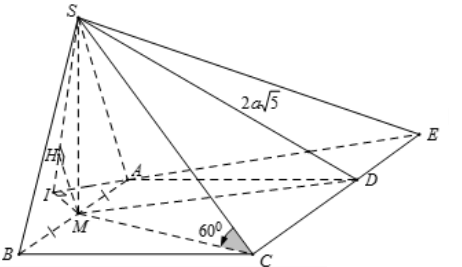
Theo giả thiết SM⊥(ABCD)⇒^(SC,(ABCD))=^SCM=60∘SM⊥(ABCD)⇒ˆ(SC,(ABCD))=ˆSCM=60∘
Dựng hình bình hành AMDEAMDE, khi đó MD//AE⇒MD//(SAE)MD//AE⇒MD//(SAE)
⇒d(MD,SA)=d(MD,(SAE))=d(M,(SAE))(1)⇒d(MD,SA)=d(MD,(SAE))=d(M,(SAE))(1) kẻ MI⊥AE(I∈AE)MI⊥AE(I∈AE) và kẻ MH⊥SI(H∈SI)MH⊥SI(H∈SI)
khi đó d(M,(SAE))=MHd(M,(SAE))=MH (2)
Ta có ABCDABCD là hình vuông nên MC=MDMC=MD, khi đó xét tam giác SMCSMC và SMDSMD ta có:
SM=MCtan60∘=√SD2−MD2⇔√3MC=√SD2−MC2⇔4MC2=SD2⇔MC=SD2=a√5SM=MCtan60∘=√SD2−MD2⇔√3MC=√SD2−MC2⇔4MC2=SD2⇔MC=SD2=a√5
⇒SM=MCtan60∘=a√15⇒SM=MCtan60∘=a√15
Xét tam giác MCBMCB ta có
BM2+BC2=MC2⇔(BC2)2+BC2=5a2⇔BC=2aBM2+BC2=MC2⇔(BC2)2+BC2=5a2⇔BC=2a
Lúc này ta sẽ tính MIMI theo 2 cách
Cách 1: Ta có cos^MA=cos^DAE⇔IMMA=ADAE⇒IM=MA⋅ADAE=a⋅2aa√5=2a√5cosˆMA=cosˆDAE⇔IMMA=ADAE⇒IM=MA⋅ADAE=a⋅2aa√5=2a√5
Cách 2: Ta có SAME=SAMD=12AM.CD=a2⇒MI=2SAMEAE=2a2a√5=2a√5SAME=SAMD=12AM.CD=a2⇒MI=2SAMEAE=2a2a√5=2a√5
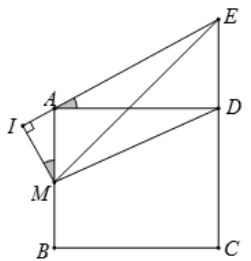
Xét tam giác SMISMI có:
1MH2=1SM2+1MI2=115a2+54a2=7960a2⇒MH=2a√15√79=2a√118579(3)1MH2=1SM2+1MI2=115a2+54a2=7960a2⇒MH=2a√15√79=2a√118579(3)
Từ (1), (2) và (3) suy ra h=d(MD,SA)=2a√118579h=d(MD,SA)=2a√118579
Đáp án B
Xem thêm các bài tiếp theo bên dưới
- Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Tính góc t
- Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2. Gọi M, N
- Cho mặt cầu ( S1 ) có bán kính R1 , mặt cầu (
- Gọi l, R, h lần lượt là độ dài đường sinh, chiều cao và bán kính đáy c
- Cho hình nón có bán kính đáy là 4 a , chiều cao 3 a . Diện tích toàn p