Cho hình hộp có đáy là hình thoi
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình hộp có đáy là hình thoi tâm , cạnh , góc . Biết rằng và cạnh bên hợp với đáy một góc bằng . Thể tích của khối đa diện bằng
Đáp án án đúng là: C
Lời giải chi tiết:
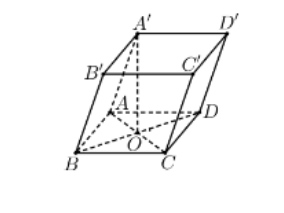
Dễ dàng tính được
Ta có
Suy ra
Đáp án C