Mạch điện xoay chiều AB gồm điện trở thuần R, cuộn cảm thuần có độ tự

Mạch điện xoay chiều AB gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L, tụ điện có điện dung C thay đổi được mắc nối tiếp theo đúng thứ tự. Điểm M nằm giữa cuộn cảm và tụ điện. Đặt vào hai đầu mạch điện một điện áp xoay chiều $\Large u=U\sqrt{2}cos\omega t (V).$ Điều chỉnh C sao cho điện áp hiệu dụng giữa hai đầu đoạn mạch MB đạt giá trị cực đại, khi đó điện áp hiệu dụng giữa hai đầu điện trở là $\Large 75V.$ Trong điều kiện đó, khi điện áp tức thời giữa hai đầu đoạn mạch AB là $\Large 75\sqrt{6}$ thì điện áp tức thời giữa hai đầu đoạn mạch AM là $\Large 25\sqrt{6}V.$ Điện áp hiệu dụng giữa hai đầu đoạn mạch AB là

• A.

  150V.

• B.

  $\Large 75\sqrt{2}V.$

• C.

  75V.

• D.

  $\Large 50\sqrt{3}V.$

Phương pháp:
+ Bài toàn C biến thiên để $\Large U_{C_{max}}$
+ Vận dụng biểu thức vuông pha
Cách giải:

C thay đổi để $\Large U_{C_{max}}$ khi đó, ta có giản đồ:

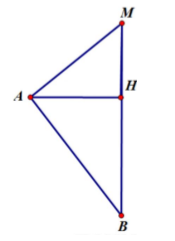
Trong đó: $\Large U_{RL} \perp U_{AB} \Rightarrow \left(\dfrac{u_{RL}}{u_{0RL}}\right)^2+\left(\dfrac{u_{AB}}{U_{0AB}}\right)^2=1 \Leftrightarrow \left(\dfrac{25\sqrt{6}}{\sqrt{2}U_{RL}}\right)^2+\left(\dfrac{75\sqrt{6}}{\sqrt{2}U_{AB}}\right)^2=1 \ (1)$   
Từ giản đồ ta có: $\Large \dfrac{1}{U_R^2}=\dfrac{1}{U_{RL}^2}+\dfrac{1}{U_{AB}^2} \Leftrightarrow \dfrac{1}{75^2}=\dfrac{1}{U_{RL}^2}+\dfrac{1}{U_{AB}^2}\ (2)$
Từ (1) và (2) ta suy ra: $\Large \left\{\begin{align} & U_{RL}=50\sqrt{3}V \\ & U_{AB}=150 V \end{align}\right.$  
Chọn A.