Khi cắt hình nón có chiều cao 16 cm và đường kính đáy 24 cm bởi một mặ

MỤC LỤC
Câu hỏi:
Khi cắt hình nón có chiều cao 16 cm và đường kính đáy 24 cm bởi một mặt phẳng song song với đường sinh của hình nón ta thu được thiết diện có diện tích lớn nhất gần nhất với giá trị nào sau đây?
Đáp án án đúng là: D
Lời giải chi tiết:
Chọn D
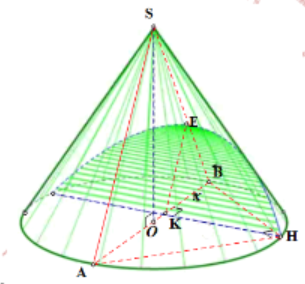
Cắt hình nón bởi một mặt phẳng song song với đường sinh của hình nón ta thu được thiết diện là một parabol.
Xét dây cung bất kỳ chứa đoạn KH như hình vẽ, suy ra tồn tại đường kính $\large AB \perp KH$, trong tam giác SAB, KE // SA, $\large E \in SB$. Suy ra Parabol nhận KE làm trục như hình vẽ chính là một thiết diện thỏa yêu cầu bài toán. (Thiết diện này song song với đường sinh SA)
Đặt BK = x (với 0 < x < 24).
Trong tam giác ABH có: $\large HK^{2} = BK.AK = x(24-x)$
Trong tam giác SAB có: $\large \dfrac{KE}{SA} = \dfrac{BK}{BA} \Leftrightarrow KE = \dfrac{BK}{BA}.SA \Leftrightarrow KE = \dfrac{5x}{6}$
Thiết diện thu được là một parabol có diện tích: $\large s = \dfrac{4}{3}KH.KE$.
Ta có:
$\large S^{2} = \dfrac{16}{9}KH^{2}.KE^{2} = \dfrac{16}{9}.x(24-x).\dfrac{25x^{2}}{36} = \dfrac{100}{81}.(24x^{3}-x^{4})$
$\large \Rightarrow S = \dfrac{10}{9}.\sqrt{24x^{3}-x^{4}}$
Đặt $\large f(x) = 24x^{3}-x^{4}$, với 0 < x < 24.
Ta có: $\large f’(x) = 72x^{2}-4x^{3}$.
Suy ra $\large f'(x) = 0\Leftrightarrow 72x^{2}-4x^{3} = 0 \Leftrightarrow \left[ \begin{align} & x=0 \\ & x= 18 \end{align} \right.$
Bảng biến thiên:
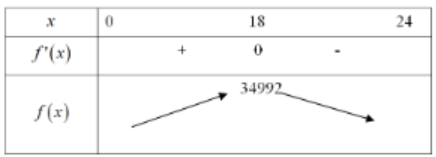
Vậy thiết diện có diện tích lớn nhất là: $\large \dfrac{10}{9}\sqrt{34992}\approx 207,8$ $\large cm^{2}
Xem thêm các bài tiếp theo bên dưới
- Cho một hình cầu nội tiếp hình nón tròn xoay có góc ở đỉnh là $\large
- Trong không gian cho bốn mặt cầu có bán kính lần lượt là 2; 3; 3; 2 (đ
- Cho khối nón có độ lớn góc ở đỉnh là $\large \dfrac{\pi }{3}$. Một khố
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên $\lar
- Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = a