Hàm số nào sau đây có đồ thị như đường cong trong hình vẽ? A. $\Large

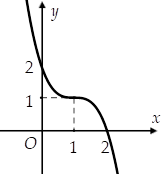
Hàm số nào sau đây có đồ thị như đường cong trong hình vẽ?

• A. A. $\Large y = x^{3} + x -1$
• B. B. $\Large y = x^{3} -3x^{2}+3x +1$
• C. C. $\Large y = -x^{3}+2$
• D. D. $\Large y = -x^{3}+3x^{2}-3x+2$

Đồ thị trong hình vẽ là dạng đồ thị của hàm số $\Large y = ax^{3}+bx^{2}+cx+d (a\neq 0)$. Dựa vào đồ thị đã cho, ta có

$\Large \cdot \underset{x\rightarrow +\infty}{\lim} y = \underset{x\rightarrow +\infty}{\lim} \left[x^{3}(\left(a+\dfrac{b}{x} + \dfrac{c}{x^{2}}+\dfrac{d}{x^{3}}\right)\right] = -\infty$ nên a<0

$\Large \cdot$ Đồ thị hàm số đi qua điểm (1; 1)

$\Large \cdot$ Tiếp tuyến với đồ thị tại điểm (1; 1) song song với trục hoành nên y'(1) = 0

Vậy hàm số thỏa mãn các yếu tố trên là $\Large y = -x^{3} + 3x^{2} - 3x + 2$