Gọi M là N lần lượt là điểm biểu diễn của các số phức $\Large z_{1}, z

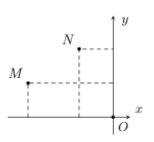
Gọi M là N lần lượt là điểm biểu diễn của các số phức $\Large z_{1}, z_{2}$ khác 0. Khi đó khẳng định nào sau đây sai?

• A. $\Large \left|z_{1}+z_{2}\right|=M N$
• B. $\Large \left|z_{2}\right|=O N$
• C. $\Large \left|z_{1}-z_{2}\right|=M N$
• D. $\Large \left|z_{1}\right|=O M$

Gọi $\Large z_{1}=a_{1}+b_{1} i \Rightarrow M\left(a_{1}, b_{1}\right), z_{2}=a_{2}+b_{2} i \Rightarrow M\left(a_{2}, b_{2}\right)$

Ta có $\Large \left|z_{1}+z_{2}\right|=\sqrt{\left(a_{1}+a_{2}\right)^{2}+\left(b_{1}+b_{2}\right)^{2}}$

Mà $\Large M N=\sqrt{\left(a_{1}-a_{2}\right)^{2}+\left(b_{1}-b_{2}\right)^{2}}$. Suy ra $\Large \left|z_{1}+z_{2}\right| \neq M N$

Chọn đáp án A