Dùng p có động năng $\Large\mathrm{K_1}$ bắn vào hạt nhân $\Large\math

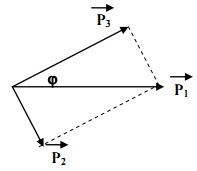
Dùng p có động năng $\Large\mathrm{K_1}$ bắn vào hạt nhân $\Large\mathrm{{}_{4}^{9}Be}$ đứng yên gây ra phản ứng: $\Large\mathrm{p+{}_{4}^{9}Be\to \alpha +{}_{3}^{6}Li}$. Phản ứng này tỏa ra năng lượng bằng W=2,1MeV . Hạt nhân $\Large\mathrm{{}_{3}^{6}Li}$và hạt $\Large\mathrm{\alpha}$ bay ra với các động năng lần lượt bằng $\Large\mathrm{K_2}$ = 3,58MeV và $\Large\mathrm{K_3}$ = 4MeV . Tính góc giữa các hướng chuyển động của hạt $\Large\mathrm{\alpha}$ và hạt p (lấy gần đúng khối lượng các hạt nhân, tính theo đơn vị u, bằng số khối).

• A.

  $\Large 45^o$

• B.

  $\Large 90^o$

• C.

  $\Large 75^o$

• D.

  $\Large 120^o$

Động năng của proton: $\Large\mathrm{K}_{1}=\mathrm{~K}_{2}+\mathrm{~K}_{3}-\Delta \mathrm{E}=5,48 \mathrm{MeV}$
Gọi P là động lượng của một vật; $\Large\mathrm{P}=\mathrm{mv} ; \mathrm{K=\dfrac{m v^{2}}{2}=\dfrac{P_{2}}{2 m}}$
$\Large\mathrm{P_1^2 = 2m_1K_1 = 2uK_1; P_2^2 = 2m_2K_2 = 12uK_2 ; P_3^2 = 2m_3K_3 = 8uK_3}$
$\Large\mathrm{{{\vec{p}}_{1}}={{\vec{p}}_{2}}+{{\vec{p}}_{3}}}$ 
$\Large\mathrm{P_{2}^{2}=P_{1}^{2}+P_{3}^{2}-2{{P}_{1}}{{P}_{3}}\cos \phi}$
$\Large\cos \varphi=\dfrac{P_{1}^{2}+P_{3}^{2}-P_{2}^{2}}{2 P_{1} P_{3}}=\dfrac{2 . K_{1}+8 K_{3}-12 K_{2}}{2 \sqrt{16 K_{1} K_{3}}}=0 \Rightarrow \varphi=90^{0} \mathrm{Chọn} \mathrm{B}$