Bắn một hạt proton có khối lượng mP vào hạt nhân $\Large\mathrm{{}_{3}

Bắn một hạt proton có khối lượng mP vào hạt nhân $\Large\mathrm{{}_{3}^{7}Li}$ đứng yên. Phản ứng tạo ra hai hạt nhân X giống nhau bay ra với vận tốc có cùng độ lớn và có phương vuông góc với nhau. Nếu xem gần đúng khối lượng hạt nhân theo đơn vị u bằng số khối của nó thì tỉ số tốc độ V’của hạt X và V của hạt proton là:

• A.

  $\Large\mathrm{\dfrac{V'}{V}=\dfrac{\sqrt{2}}{4}}$

• B.

  $\Large\mathrm{\dfrac{V'}{V}=\dfrac{1}{4}}$

• C.

  $\Large\mathrm{\dfrac{V'}{V}=\dfrac{\sqrt{2}}{8}}$

• D.

  $\Large\mathrm{\dfrac{V'}{V}=\dfrac{1}{2}}$

Giải 1: $\Large\mathrm{{}_{1}^{1}p+{}_{3}^{7}Li\to 2{}_{2}^{4}X}$
Theo ĐL bảo toàn động lượng : $\Large\mathrm{\vec{p}={{\vec{p}}_{1}}+{{\vec{p}}_{2}}}$ mà : $\Large\mathrm{p_1 = p_2 = m_Xv’}$ ;
$\Large\mathrm{{{\vec{p}}_{1}}\bot {{\vec{p}}_{2}}}$
$\Large\mathrm{\Rightarrow p_2 = p_{1}^{2}+p_{2}^{2} \Rightarrow (m_Pv)^2 = 2(m_Xv’)^2}$
$\Large\mathrm{\Rightarrow v = \sqrt{2} .4.v’ => v’/v = 1/\sqrt{2} .4 \Rightarrow}$ $\Large\mathrm{\frac{V'}{V}=\frac{\sqrt{2}}{8}}$ 
ĐÁP ÁN C

Giải 2:
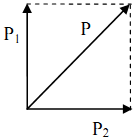
+ Bảo toàn động lượng ta có: $\Large\mathrm{{{\vec{p}}_{P}}={{\vec{p}}_{{{X}_{1}}}}{{\vec{p}}_{{{X}_{2}}}}\Rightarrow p_{P}^{2}=p_{X}^{2}+p_{X}^{2}+2p_{X}^{2}\cos {{90}^{0}}}$
$\Large\mathrm{\Rightarrow {{p}_{P}}=\sqrt{2}{{p}_{X}}\Rightarrow {{A}_{P}}.V=\sqrt{2}{{A}_{X}}.V'\Rightarrow \frac{V'}{V}=\dfrac{1}{4\sqrt{2}}=\dfrac{\sqrt{2}}{8}}$