Đặt điện áp xoay chiều $\Large\ u = U_0 cos(2 \pi ft)$ ($\Large\ U

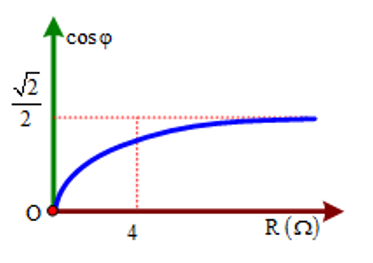
Đặt điện áp xoay chiều $\Large\ u = U_0 cos(2 \pi ft)$ ($\Large\ U_0, f$ không đổi) vào hai đầu đoạn mạch có R, L, C mắc nối tiếp trong đó R thay đổi được. Đồ thị biểu diễn sự phụ thuộc hệ số công suất theo R. Hệ số công suất của mạch khi $\Large\ R=\dfrac{4\sqrt{3}}{3}\Omega $ là? 

• A.

  A. 0,5

• B.

  B. 0,87

• C.

  C. 0,59

• D.

  D. 0,71

+ Hệ số công suất của mạch: $\Large\ \cos \varphi =\dfrac{R}{Z}=\dfrac{R}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\dfrac{1}{\sqrt{1+\dfrac{{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}{{{R}^{2}}}}}$ 
+ Khi $\Large\ R=4\Rightarrow \cos \varphi =\dfrac{\sqrt{2}}{2}\Rightarrow {{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}=16$ 
+ Khi $\Large\ R=\dfrac{4\sqrt{3}}{3}\Omega \Rightarrow \cos \varphi =\dfrac{\dfrac{4\sqrt{3}}{3}}{\sqrt{{{\left( \dfrac{4\sqrt{3}}{3} \right)}^{2}}+16}}=\dfrac{1}{2}$ 
→ Đáp án A