Con lắc gồm lò xo nhẹ gắn cố định một đầu, đầu kia treo vật nhỏ tại nơ

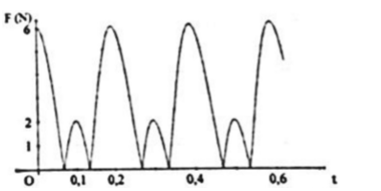
Con lắc gồm lò xo nhẹ gắn cố định một đầu, đầu kia treo vật nhỏ tại nơi có gia tốc rơi tự do $\Large g=10m/s^2.$ Khi con lắc dao động điều hòa theo phương thẳng đứng, lực đàn hồi trên lò xo có độ lớn được biểu diễn bằng đồ thị như hình vẽ. Biết gốc tọa độ tại vị trí cân bằng, chiều dương hướng lên, lấy  Phương trình dao động của con lắc là

• A.

  $\Large x=6cos(10\pi t+\pi) (cm).$

• B.

  $\Large x=4cos\left(10\pi t+\dfrac{\pi}{2}\right) (cm).$

• C.

  $\Large x=2cos(10\pi t+\pi) (cm).$

• D.

  $\Large x=6cos(10\pi t) (cm).$

Phương pháp:
+ Đọc đồ thị F-t
+ Sử dụng biểu thức tính lực đàn hồi $\Large F_{\text{đh}}=k(\Delta l+x)$
+ Vận dụng biểu thức: $\Large T=2\pi \sqrt{\dfrac{\Delta l}{g}}$
+ Viết phương trình dao động
Cách giải:
Từ đồ thị, ta có:
+ Chu kì dao động: $\Large T=0,2s \Rightarrow \omega =\dfrac{2\pi}{T}=10\pi (rad/s)$
+ Lực đàn hồi tại biên âm: $\Large F_{\text{đh max}}=k(\Delta l+A)=6N \ (1)$
+ Lực dàn hồi tại biên dương: $\Large F_{\text{đh}}=k(A-\Delta l)=2N \ (2)$
Lấy $\Large \dfrac{(1)}{(2)}$ ta được $\Large \dfrac{\Delta l+A}{A-\Delta l}=3 \Rightarrow A=2\Delta l$ 
Lại có: $\Large \Delta l=\dfrac{T^2g}{4\pi^2}=\dfrac{0,2^2.10}{4\pi^2}=0,01m=1cm \Rightarrow A=2cm$
Tại thời điểm ban đầu, vật đang ở biên âm $\Large \Rightarrow \varphi=\pi$
$\Large \Rightarrow$ Phương trình dao động của con lắc: $\Large x=2cos(10\pi t+\pi) (cm)$
Chọn C.