Có bao nhiêu số nguyên thỏa mãn bất phương trình $\Large 2.3^{x+\sqrt{

Có bao nhiêu số nguyên thỏa mãn bất phương trình $\Large 2.3^{x+\sqrt{x}}+9^{\sqrt{x}+\dfrac{1}{2}}\geq 9^x$?

• A.

  A. 3

• B.

  B. 4

• C.

  C. 5

• D.

  D. 6

Chọn A

Điều kiện $\Large \begin{align}&x\geq0\\&2.3^{x+\sqrt{x}}+9^{\sqrt{x}+\dfrac{1}{2}}\geq 9^x\Leftrightarrow 2.3^x.3^{\sqrt{x}}+3.\left(3^{\sqrt{x}}\right)^2\geq (3^x)^2\Leftrightarrow 2.\dfrac{3^{\sqrt{x}}}{3^x}+3.\left(\dfrac{3^{\sqrt{x}}}{3^x}\right)^2\geq1\Leftrightarrow 2.3^{\sqrt{x}-x}+3.\left(3^{\sqrt{x}-x}\right)^2\geq1\end{align}$

Đặt $\Large t=3^{\sqrt{x}-x}\geq 0 $, ta có $\Large 3t^2+2t-1\geq0$

Suy ra $\Large t\geq\dfrac{1}{3}\Leftrightarrow 3^{\sqrt{x}-x}\geq 3^{-1}\Leftrightarrow \sqrt{x}-x\geq -1\Leftrightarrow -(\sqrt{x})^2+\sqrt{x}+1\geq0$

Đặt $\Large u=\sqrt{x}\geq0$, ta có $\Large -u^2+u+1\geq0$

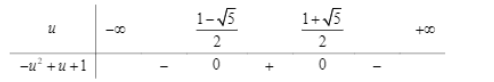
Khi đó $\Large 0\leq u\leq \dfrac{1+\sqrt{5}}{2}\Leftrightarrow 0\leq \sqrt{x}\leq\dfrac{1+\sqrt{5}}{2}\Leftrightarrow 0\leq x\leq \dfrac{3+\sqrt{5}}{2}$

Tập nghiệm nguyên $\Large T=\left\{0; 1; 2\right\}$