Cho tứ diện S.ABC, M và N là các điểm thuộc các cạnh SA và SB sao cho

MỤC LỤC
Câu hỏi:
Cho tứ diện S.ABC, M và N là các điểm thuộc các cạnh SA và SB sao cho MA=3SM,SN=2NBMA=3SM,SN=2NB, (α)(α) là mặt phẳng qua MN và song song với SC. Kí hiệu (H1)(H1) và (H2)(H2) là các khối đa diện có được khi chia khối tứ diện S.ABC bởi mặt phẳng (α)(α), trong đó, (H1)(H1) chứa điểm S, (H2)(H2) chứa điểm A; V1V1 và V2V2 lần lượt là thể tích của (H1)(H1) và (H2)(H2). Tính tỉ số V2V1+2V2V2V1+2V2
Đáp án án đúng là: A
Lời giải chi tiết:
Chọn A
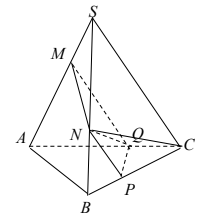
Kẻ NP//SC(P∈BC)NP//SC(P∈BC), kẻ MQ//SC(Q∈SC)MQ//SC(Q∈SC)
Khi đó, mặt phẳng (α)(α) cắt hình chóp theo thiết diện là MNPQ.
Vì NP//SC⇒CPCB=23;MQ//SC⇒CQCA=14.NP//SC⇒CPCB=23;MQ//SC⇒CQCA=14.
Ta có SΔCPQSΔCBA=CPCB⋅CQCA=14⋅23=16⇒SΔCPQ=16S△ABCSΔCPQSΔCBA=CPCB⋅CQCA=14⋅23=16⇒SΔCPQ=16S△ABC
Và d(N;(ABC))=13d(S;(ABC))⇒VN.CPQ=118VS.ABC=V18d(N;(ABC))=13d(S;(ABC))⇒VN.CPQ=118VS.ABC=V18
Lại có SΔAAMQSΔAASC=AMSA⋅AQAC=34⋅34=916⇒SSMQC =716S△SACSΔAAMQSΔAASC=AMSA⋅AQAC=34⋅34=916⇒SSMQC =716S△SAC
Và d(N;(SAC))=23d(B;(SAC))⇒VN.SMQC=724Vd(N;(SAC))=23d(B;(SAC))⇒VN.SMQC=724V
Do đó V1=VSCMNPQ =VN.CPQ+VN. SMQC =V18+7V24=25V72⇒V2=47V72V1=VSCMNPQ =VN.CPQ+VN. SMQC =V18+7V24=25V72⇒V2=47V72
Vậy tỉ số V2V1+2V2=47V7225V72+2⋅47V72=47119.V2V1+2V2=47V7225V72+2⋅47V72=47119.
Xem thêm các bài tiếp theo bên dưới
- Cho hàm số $\Large f(x)=\left(a^{2}+1\right) \ln ^{2019}\left(x+\sqrt{
- Cho hàm số y=f(x)y=f(x) có đạo hàm liên tục trên R
- Gọi S là tập hợp tất cả các số nguyên m để hàm số $\Large y=\left|\dfr
- Cho hàm số y=f(x), hàm số y=f′(x) liên tục t
- Một câu hỏi trắc nghiệm một lựa chọn có một phương án đúng, ba phương