Cho hàm số $\Large y=f(x)$, hàm số $\Large y=f^{\prime}(x)$ liên tục t

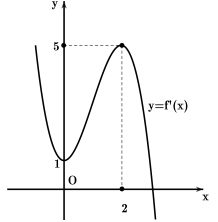
Cho hàm số $\Large y=f(x)$, hàm số $\Large y=f^{\prime}(x)$ liên tục trên $\Large \mathbb R$ và có đồ thị như hình vẽ.

Bất phương trình $\Large f(x) > m+x^{3}-3 x^{2}+8 x$ ( m là tham số thực) nghiệm đúng với mọi $\Large x \in(0 ; 3)$ khi và chỉ khi

• A. $\Large m < f(0)$
• B. $\Large m < f(3)-24$
• C. $\Large m \leq f(0)$
• D. $\Large m \leq f(3)-24$

Chọn D

Ta có $\Large f(x) > m+x^{3}-3 x^{2}+8 x \Leftrightarrow m < f(x)-x^{3}+3 x^{2}-8 x$

Xét hàm số $\Large g(x)=f(x)-x^{3}+3 x^{2}-8 x$ có

$\Large g^{\prime}(x)=f^{\prime}(x)-3 x^{2}+6 x-8$

$\Large g^{\prime}(x)=0$ $\Large \Leftrightarrow f^{\prime}(x)-3 x^{2}+6 x-8=0 \Leftrightarrow f^{\prime}(x)=3 x^{2}-6 x+8$

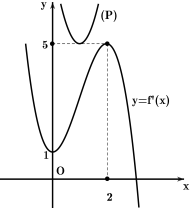
Từ đồ thị hàm số $\Large y=f^{\prime}(x)$ và parabol $\Large (P): y=3 x^{2}-6 x+8$ suy ra $\Large f^{\prime}(x) < 3 x^{2}-6 x+8$ với mọi $\Large x \in(0 ; 3)$

Suy ra $\Large g^{\prime}(x)=f^{\prime}(x)-3 x^{2}+6 x-8 < 0, \forall x \in(0 ; 3)$

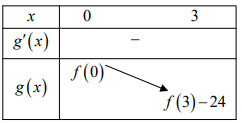
Vậy bất phương trình $\Large f(x) > m+x^{3}-3 x^{2}+8 x$ ( m là tham số thực) nghiệm đúng với mọi $\Large x \in(0 ; 3)$ khi và chỉ khi $\Large m \leq f(3)-24$