Cho hàm số $\Large y=f(x)$ có đạo hàm liên tục trên $\Large \mathbb R$

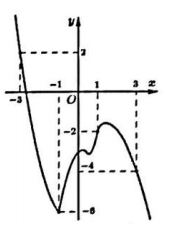
Cho hàm số $\Large y=f(x)$ có đạo hàm liên tục trên $\Large \mathbb R$. Đồ thị hàm số $\Large y=f^{\prime}(x)$ như hình bên

Hỏi hàm số $\Large g(x)=2 f(x)+(x+1)^{2}$ đồng biến trên khoảng nào trong các khoảng sau?

• A. (-3;1)
• B. (1;3)
• C. $\Large (-\infty ; 3)$
• D. $\Large (3 ;+\infty)$

Chọn B

Ta có $\Large g(x)=2 f(x)+(x+1)^{2} \Rightarrow g^{\prime}(x)=2 f^{\prime}(x)+2(x+1)$

Suy ra $\Large g^{\prime}(x) > 0 \Leftrightarrow 2 f^{\prime}(x)+2(x+1) > 0 \Leftrightarrow f^{\prime}(x) > -x-1$

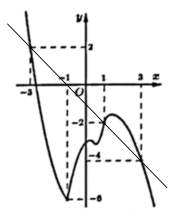
Từ đồ thị hàm số $\Large y=f^{\prime}(x)$ ta suy ra hàm số $\Large g(x)=2 f(x)+(x+1)^{2}$ đồng biến trên khoảng $\Large (1 ;3)$