Gọi S là tập hợp tất cả các số nguyên m để hàm số $\Large y=\left|\dfr

Gọi S là tập hợp tất cả các số nguyên m để hàm số $\Large y=\left|\dfrac{1}{4} x^{4}-\dfrac{19}{2} x^{2}+30 x+m\right|$ có giá trị lớn nhất trên đoạn [0;2] không vượt quá 20. Tổng các phân tử của S là

• A. -195
• B. 195
• C. 210
• D. -210

Xét hàm số $\Large u(x)=\frac{1}{4} x^{4}-\frac{19}{2} x^{2}+30 x+m$$\Large \Rightarrow u^{\prime}(x)=x^{3}-19 x+30 \Rightarrow u^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}
x=-5 \\
x=2 \\
x=3
\end{array}\right.$

Bảng biến thiên

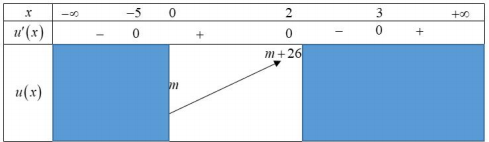
Suy ra $\Large \max _{[0 ; 2]} u(x)=m+26 ; \min _{[0 ; 2]} u(x)=m$

Do đó $\Large \max _{[0 ; 2]} y=\max _{[0 ; 2]}|u(x)|=\max \{|m| ;|m+26|\}$

Vậy $\Large \Rightarrow\left\{\begin{array}{l}
|m| \leq 20 \\
|m+26| \leq 20
\end{array} \Leftrightarrow\left\{\begin{array}{l}
-20 \leq m \leq 20 \\
-20 \leq m+26 \leq 20
\end{array}\right.\right.$$\Large \Leftrightarrow\left\{\begin{array}{l}
-20 \leq m \leq 20 \\
-46 \leq m \leq-6
\end{array} \Leftrightarrow-20 \leq m \leq-6\right.$

Mà $\Large m \in \mathbb Z \Rightarrow m \in S=\{-20 ;-19 ; \ldots ;-6\}$. Tổng các phân tử của S là -195.