Cho tứ diện $\large ABCD$ có $\large AB=x,AC=AD=CB=DB=2\sqrt{3}$ , kho

Cho tứ diện $\large ABCD$ có $\large AB=x,AC=AD=CB=DB=2\sqrt{3}$ , khoảng cách giữa $\large AB,CD$ bằng 1. Tìm $\large x$ để khối tứ diện $\large ABCD$ có thể tích lớn nhất

• A.

  A. $\large x=\sqrt{22}$

• B.

  B. $\large x=\sqrt{13}$

• C.

  C. $\large x=\sqrt{26}$

• D.

  D. $\large x=\sqrt{11}$

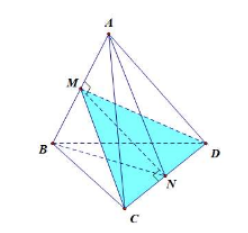
Gọi $\large M,N$ lần lượt là trung điểm của các cạnh $\large AB$ và $\large CD$

$\large \Delta  ACD$ cân tại $\large A$ (vì $\large AC=AD$) nên  $\large AN\perp CD$

$\large \Delta  BCD$ cân tại $\large B$ (vì $\large BD=BC$) nên $\large BN\perp CD$

Suy ra $\large CD\perp (ABN)\Rightarrow MN\perp CD$

Tương tự, ta cũng có $\large MN\perp AB$. Do đó $\large MN$ là đoạn vuông góc chung của hai đường thẳng $\large AB$ và $\large CD$ suy ra $\large d(AB,CD)=MN=1$

$\large\bigtriangleup CMD$ cân tại $\large M$ cho $\large MC^{2}=MD^{2}=BC^{2}-MB^{2}=12-\dfrac{x^{2}}{4}$

Và $\large MN^{2}=\dfrac{2(MC^{2}+MD^{2})-CD^{2}}{4}\Rightarrow CD=\sqrt{44-x^{2}}$

Mà $\large V_{ABCD}=2V_{A.MCD}=2\cdot \dfrac{1}{3}S_{\bigtriangleup MCD}.AM=\dfrac{1}{3}MN.CD.AM=\dfrac{1}{3}\cdot \dfrac{x}{2}\sqrt{44-x^{2}}=\dfrac{1}{6}x\sqrt{44-x^{2}}$

Theo bất đẳng thức $\large AM-GM$ ta có $\large x\sqrt{44-x^{2}}\leq \dfrac{x^{2}+\left ( \sqrt{44-x^{2}} \right )^{2}}{2}=22$

Suy ra $\large V_{ABCD}\leq \dfrac{1}{6}\cdot 22=\dfrac{11}{3}\Rightarrow max(V_{ABCD})=\dfrac{11}{3}$

Dấu "=" xảy ra khi $\large x=\sqrt{44-x^{2}}\Rightarrow x=\sqrt{22}$

Vậy khi $\large x=\sqrt{22}$ thì thể tích khối chóp $\large ABCD$ đạt giá trị lớn nhất

Đáp án A