Cho số phức z thỏa mãn $\Large |z|=\sqrt{2}$. Biết điểm A tronng hình

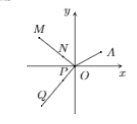
Cho số phức z thỏa mãn $\Large |z|=\sqrt{2}$. Biết điểm A tronng hình dưới đây biểu diễn số phức z. Hỏi điểm nào tron hình bên biểu diễn só phức $\Large w=\dfrac{1}{i z}$

• A. Điểm M
• B. Điểm N
• C. Điểm P
• D. Điểm Q

Gọi $\Large z=x+y i(x, y \in R )$. Dựa vào các điểm A ta có $\Large x>y>0$

$\Large |w|=\left|\dfrac{1}{i z}\right|=\dfrac{1}{1 \cdot|z|}=\dfrac{1}{\sqrt{2}}

$\Large w=\dfrac{1}{i z}=\dfrac{1}{i(x+y i)}=\dfrac{1}{-(y-x i)}=\dfrac{-(y+x i)}{y^{2}+x^{2}}=\dfrac{-y}{x^{2}+y^{2}}+\dfrac{-x}{x^{2}+y^{2}} i$

Phần thực và phần ảo của w đều âm nên diểm P thỏa mãn 

Chọn đáp án C