Cho mặt cầu ( S ) tâm O , bán kính R = 3. Mặt phẳng ( P ) cách O một k

Cho mặt cầu (S) tâm O, bán kính R = 3. Mặt phẳng (P) cách O một khoảng bằng 1 và cắt (S) theo giao tuyến là đường tròn (C) có tâm H. Gọi T  là giao điểm của tia HO với (S), tính thể tích V của khối nón có đỉnh T  và đáy là hình tròn (C).

• A.

  A. $\large V = \dfrac{32\pi }{3}$

• B.

  B. $\large V = 16\pi$

• C.

  C. $\large V = \dfrac{16\pi }{3}$

• D.

  D. $\large V = 32\pi$

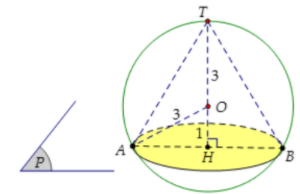
Gọi AB là đường kính của đường tròn (C). Khi đó:

$\large  R_{non}^{2} = AH^{2} = OA^{2}-OH^{2} = 3^{2}-1^{2} = 8$ 

Ta có chiều cao của nón: h = TH = TO+OH = 3+1  = 4.

Suy ra thể tích của khối nón:

$\large  V = \dfrac{1}{3}h\pi R_{non}^{2} = \dfrac{1}{3}4\pi .8 = \dfrac{32\pi }{3}$