Cho hình trụ có hai đáy là hai hình tròn ( O ) và ( O’ ), chiều cao $\
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình trụ có hai đáy là hai hình tròn (O) và (O’), chiều cao R√3R√3 và bán kính đáy R. Một hình nón có đỉnh là O’ và đáy là hình tròn (O;R). Tỷ số diện tích xung quanh của hình trụ và hình nón bằng:
Đáp án án đúng là: C
Lời giải chi tiết:
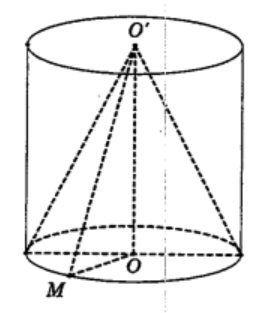
Diện tích xung quanh của hình trụ:
Sxq(T)=2πR.h=2πR.R√3=2√3πR2Sxq(T)=2πR.h=2πR.R√3=2√3πR2 (đvdt).
Kẻ đường sinh O’M của hình nón, suy ra
l = O’M = √OO′2+OM2=√3R2+R2=2R.
Diện tích xung quanh của hình nón:
Sxq(N)=πRl=πR.2R=2πR2 (đvdt).
Vậy Sxq(T)Sxq(N)=√3. Chọn C.
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa mặt bê
- Diện tích toàn phần của hình nón có khoảng cách từ tâm của đáy đến đườ
- Thiết diện qua trục của một hình nón là một tam giác vuông cân có diện
- Cho hình chóp lục giác đều S.ABCDEF có cạnh bên bằng 2 a và tạo với đá
- Cho lăng trụ đứng ABC.A’B’C’ có cạnh bên AA’ = 2a . Tam giác ABC vuông