Cho lăng trụ đứng ABC.A’B’C’ có cạnh bên AA’ = 2a . Tam giác ABC vuông
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho lăng trụ đứng ABC.A’B’C’ có cạnh bên AA’ = 2a. Tam giác ABC vuông tại A có $\large BC = 2a\sqrt{3}$. Thể tích của hình trụ ngoại tiếp khối lăng trụ này là:
Đáp án án đúng là: A
Lời giải chi tiết:
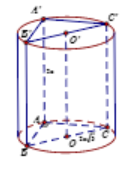
Ta có: $\large R = a\sqrt{3}$ và h = 2a.
Áp dụng công thức:
$\large V = \pi R^{2}h = \pi .(a\sqrt{3})^{2}.2a = 6\pi a^{3}$
Vậy chọn đáp án A.
Xem thêm các bài tiếp theo bên dưới
- Cho ABB’A’ là thiết diện song song với trục OO’ của hình trụ ( A, B th
- Trong không gian, cho tam giác ABC vuông tại A, AB = a và diện tích ta
- Thiết diện qua trục của một hình nón là tam giác đều cạnh bằng 2. Một
- Cho hình chóp tứ giác đều S.ABCD có các cạnh đều bằng $\large a\sqrt{2
- Cho tứ diện đều ABCD cạnh bằng a . Diện tích xung quanh $\large S_{xq}