Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa mặt bê
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa mặt bên và đáy bằng 60∘. Thể tích khối nón nội tiếp trong hình chóp là:
Đáp án án đúng là: B
Lời giải chi tiết:
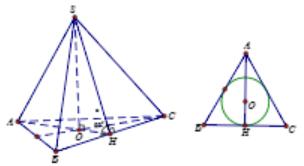
Áp dụng công thức
V=13πR2h
Với R=OH=13AH=13.a√32=a√36
h=SO=OH.tan60∘=a2
Vậy V=13πR2h=13π(a√36).a2=πa372
Vậy chọn đáp án B.
Xem thêm các bài tiếp theo bên dưới
- Diện tích toàn phần của hình nón có khoảng cách từ tâm của đáy đến đườ
- Thiết diện qua trục của một hình nón là một tam giác vuông cân có diện
- Cho hình chóp lục giác đều S.ABCDEF có cạnh bên bằng 2 a và tạo với đá
- Cho lăng trụ đứng ABC.A’B’C’ có cạnh bên AA’ = 2a . Tam giác ABC vuông
- Cho ABB’A’ là thiết diện song song với trục OO’ của hình trụ ( A, B th