Cho hình trụ có bán kính đáy và trục $\Large OO'$ cùng độ dài bằng

Cho hình trụ có bán kính đáy và trục $\Large OO'$ cùng độ dài bằng 1. Một mặt phẳng $\Large (P)$ thay đổi đi qua $\Large O$, tạo với đáy của hình trụ một góc $\Large 60^{\circ}$ và cắt hai đáy của hình trụ đã cho theo hai dây cung $\Large AB$ và $\Large CD$($\Large AB$ qua $\Large O$). Tính diện tích của tứ giác $\Large ABCD$.

• A.

  $\Large \dfrac{\sqrt{3}+\sqrt{2}}{2}$.

• B.

  $\Large \dfrac{3\sqrt{3}+3\sqrt{2}}{2}$.

• C.

  $\Large 2\sqrt{3}+2\sqrt{2}$.

• D.

  $\Large \dfrac{2\sqrt{3}+2\sqrt{2}}{3}$.

Chọn D

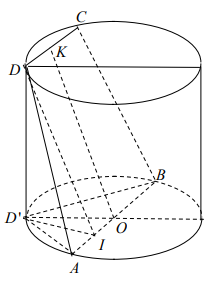
Dễ thấy $\Large ABCD$ là hình thang cân có $\Large AB// CD$ đáy lớn $\Large AB$ (hình vẽ).

Gọi $\Large D'$ là hình chiếu vuông góc của D trên mặt phẳng chứa đường tròn (O). Dựng $\Large D'I\perp AB\Rightarrow AB\perp (DID')$

Do đó $\Large (ABCD); \big((O)\big)=DID'=60^{\circ}$; $\Large AB=2R=2$.

Suy ra $\Large DIsin60^{\circ}=DD'$ $\Large \Rightarrow DI=\dfrac{2}{\sqrt{3}}DD'=\dfrac{2}{\sqrt{3}}$.

$\Large D'I=\sqrt{DI^2-DD'^2}=\dfrac{1}{3}$.

Ta có: $\Large IA(2-IA)=D'I^2=\dfrac{1}{3}$ $\Large \Rightarrow IA=\dfrac{3-\sqrt{6}}{3}$ (Do $\Large IA < R=1$) $\Large CD=AB-2AI=\dfrac{2\sqrt{6}}{3}$.

Diện tích hình thang $\Large ABCD$ là $\Large S=\dfrac{AB+CD}{2}.DI=\dfrac{2\sqrt{3}+2\sqrt{2}}{3}$.