Cho hình hộp $\Large ABCD.A'B'C'D'$ có đáy $\Large ABCD$ là hình chữ n

Cho hình hộp $\Large ABCD.A'B'C'D'$ có đáy $\Large ABCD$ là hình chữ nhật có diện tích bằng $\Large \sqrt{3}$. Tính thể tích $\Large V$ của khối biết $\Large CC'=\sqrt{7}$, các mặt phẳng $\Large (ABB'A')$ và $\Large (ADD'A')$ lần lượt tạo với mặt đáy $\Large (ABCD)$ các góc $\Large 45^{\circ}$ và $\Large 60^{\circ}$.

• A.

  $\Large V=3$.

• B.

  $\Large V=7\sqrt{3}$.

• C.

  $\Large V=\sqrt{21}$.

• D.

  $\Large V=3\sqrt{7}$.

Chọn A

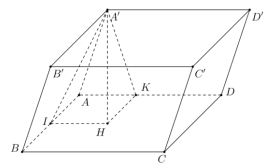
Gọi $\Large H$ là hình chiếu của điểm $\Large A'$ lên mặt phẳng $\Large (ABCD)$, $\Large I, K$ lần lượt là hình chiếu của $\Large H$ lên các cạnh $\Large AB$ và $\Large AD$.

Khi đó, ta xác định được $\Large \big((ABB'A'); (ABCD)\big)=A'IH=45^{\circ}$, $\Large \big((ADD'A'); (ABCD)\big)=A'KH=60^{\circ}$.

Đặt $\Large A'H=x > 0$.

Ta có $\Large tanA'IH=\dfrac{A'H}{IH}=1$ $\Large \Rightarrow A'H=IH=x$, $\Large tanA'KH=\dfrac{A'H}{HK}=\sqrt{3}$ $\Large \Rightarrow HK=\dfrac{x}{\sqrt{3}}$.

Lại có $\Large AH^2=IH^2+HK^2=x^2+\dfrac{x^2}{3}=\dfrac{4x^2}{3}$.

Xét $\Large \Delta AA'H$ có $\Large AA'^2=A'H^2+AH^2$ $\Large \Leftrightarrow 7=x^2+\dfrac{4x^2}{3}$ $\Large \Leftrightarrow 21=7x^2$ $\Large \Leftrightarrow x=\sqrt{3}$.

Vậy $\Large V_{ABCD.A'B'C'D'}=S_{ABCD}.A'H=\sqrt{3}.\sqrt{3}=3$.