Cho hình nón đỉnh S có đáy là hình tròn tâm O , bán kính R . Dựng hai

Cho hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R. Dựng hai đường sinh SA và SB,biết AB chắn trên đường tròn đáy một cung có số đo bằng $\large 60^{\circ}$, khoảng cách từ tâm O đến mặt phẳng (SAB) bằng $\large \dfrac{R}{2}$. Đường cao h của hình nón bằng:

• A.

  A. $\large h = \dfrac{R\sqrt{6}}{4}$

• B.

  B. $\large h = \dfrac{R\sqrt{3}}{2}$

• C.

  C. $\large h = a\sqrt{3}$

• D.

  D. $\large h = a\sqrt{2}$

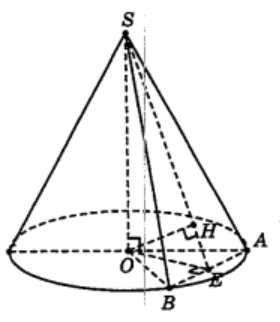
Theo giả thiết ta có tam giác OAB đều cạnh R. 

Gọi E là trung điểm AB, suy ra $\large OE \perp AB$ và $\large OE = \dfrac{R\sqrt{3}}{2}$.

Gọi H là hình chiếu của O trên SE, suy ra $\large OH \perp SE$.

Ta có: $\large \left\{\begin{matrix} AB \perp OE & \\  AB \perp SO &  \end{matrix}\right.\Rightarrow AB \perp (SOE)\Rightarrow AB \perp OH$ 

Từ đó suy ra $\large OH \perp (SAB)$ nên d[O,(SAB)] = OH = $\large \dfrac{R}{2}$ 

Trong tam giác vuông SOE, ta có:

$\large \dfrac{1}{SO^{2}} = \dfrac{1}{OH^{2}}-\dfrac{1}{OE^{2}} = \dfrac{8}{3R^{2}}\Rightarrow SO = \dfrac{R\sqrt{6}}{4}$ 

Chọn A.