Cho hình lăng trụ $\large ABCD.A'B'C'D'$ có đáy $\large ABCD$ là hình

Cho hình lăng trụ $\large ABCD.A'B'C'D'$ có đáy $\large ABCD$ là hình chữ nhật $\large AB=a,AD=a\sqrt{3}$ . Hình chiếu vuông góc của $\large A'$ trên mặt phẳng $\large (ABCD)$ trùng với giao điểm của $\large AC$ và $\large BD$. Góc giữa hai mặt phẳng $\large (ADD'A')$ và $\large (ABCD)$ bằng $\large 60^{\circ}$ . Tính thể tích khối tứ diện $\large ACB'D'$

• A.

  A. $\large\dfrac{a^{3}}{3}$

• B.

  B. $\large\dfrac{3a^{3}}{2}$

• C.

  C. $\large\dfrac{a^{3}}{2}$

• D.

  D. $\large\dfrac{a^{3}}{6}$

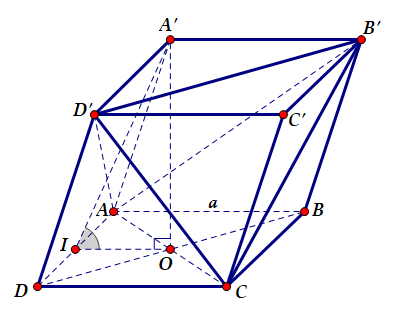
Gọi $\large O=AC\cap BD$ và $\large I$ là trung điểm $\large AD$

Ta có $\large (ADD'A')\cap (ABCD)=AD,OI\perp AD$ và $\large A'O\perp (ABCD)$ nên góc giữa hai mặt phẳng $\large (ADD'A')$ và $\large (ABCD)$ là $\large \widehat{A'IO}=60^{\circ}$

Tam giác $\large A'IO$ vuông tại $\large O$ nên $\large A'O=IO\tan \widehat{A'IO}=\dfrac{a}{2}.\tan 60^{\circ}=\dfrac{a\sqrt{3}}{2}$

Thể tích của khối lăng trụ $\large ABCD.A'B'C'D'$ là $\large V=AB.AD.A'O=a\cdot a\sqrt{3}\cdot \dfrac{a\sqrt{3}}{2}=\dfrac{3a^{3}}{2}$

Dễ thấy $\large V_{CC'B'D'}=V_{B'.ABC}=V_{D'.ACD}=V_{A.A'B'D'}=\dfrac{1}{3}\cdot \dfrac{1}{2}AD.DC.A'O=\dfrac{1}{6}\cdot a\sqrt{3}\cdot a\cdot \dfrac{a\sqrt{3}}{2}=\dfrac{a^{3}}{4}$ 

Thể tích khối tứ diện $\large ACB'D'$ là

$\large V_{A.CB'D'}=V-V_{C.C'B'D'}-V_{B'.ABC}-V_{D'.ACD}-V_{A.A'B'D'}=V-4V_{D'.ACD}=\dfrac{3a^{3}}{2}-4\cdot \dfrac{a^{3}}{4}=\dfrac{a^{3}}{2}$

Đáp án C