Cho hình chóp tứ giác S.ABCD có đáy là hình thoi cạnh a, AC = a và $\l

Cho hình chóp tứ giác S.ABCD có đáy là hình thoi cạnh a, AC = a và $\large SA=SB=SC=a\sqrt{2}$. Bán kính mặt cầu ngoại tiếp tứ diện SACD là

• A.

  $\large \dfrac{3a}{2}$

• B.

  $\large a\sqrt{2}$

• C.

  $\large a\sqrt{3}$

• D.

  $\large \dfrac{a\sqrt{3}}{2}$

Chọn D

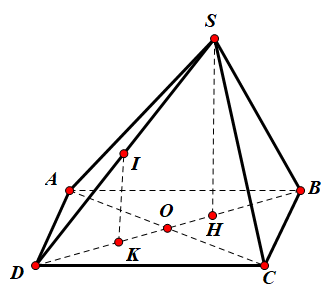
Gọi $\large O=AC\cap BD$

Do tam giác ABC đều và $\large SA=SB=SC=a\sqrt{2}$ nên S.ABC là hình chóp tam giác đều

Gọi H là trọng tâm của tam giác đều ABC ta có $\large SH\perp (ABC)$

Gọi K là trọng tâm của tam giác đều ACD, qua K dựng trục đường tròn $\large \Delta$ ngoại tiếp tam giác ACD thì $\large \Delta // SH$ và $\large \Delta \cap SD=I$

Vì $\large I\in \Delta$ nên $\large IA=IC=ID$ (1)

Mặt khác: $\large \Delta // SH$ và $\large DK=KH=\dfrac{2}{3}OD=\dfrac{a\sqrt{3}}{3}$ nên I là trung điểm của SD hay IS = ID (2)

Từ (1) và (2) ta có I là tâm mặt cầu ngoại tiếp tứ diện SACD, bán kính mặt cầu R = DI

Tam giác vuông SHB có $\large SH=\sqrt{SB^2-BH^2}=\sqrt{\left(a\sqrt{2} \right )^2-\left(\dfrac{a\sqrt{3}}{3} \right )^2}=\dfrac{a\sqrt{15}}{3}$

Mà $\large IK=\dfrac{1}{2}SH=\dfrac{a\sqrt{15}}{6}$

Vậy bán kính mặt cầu ngoại tiếp tứ diện SACD là

$\large R=DI=\sqrt{DK^2+IK^2}=\sqrt{\left(\dfrac{a\sqrt{3}}{3} \right )^2+\left(\dfrac{a\sqrt{15}}{6} \right )^2}=\dfrac{a\sqrt{3}}{2}$