Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A, $\lar

Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A, $\large AB=a, \,\, ACB=30^\circ$ và $\large SA=SB=SD$ với D là trung điểm của BC. Cạnh SA hợp với đáy một góc $\large 45^\circ$. Thể tích khối chóp đã cho bằng: 

• A. A. $\large \dfrac{a^3}{12}$
• B. B. $\large \dfrac{a^3}{2}$
• C. C. $\large \dfrac{a^3}{6}$
• D. D. $\large \dfrac{a^3}{4}$

Chọn C

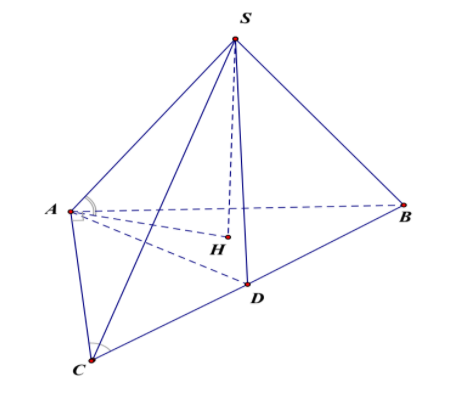
Ta có: $\large ACB=60^\circ\Rightarrow ABC=60^\circ$

$\large AB=a\Rightarrow BC=2c\Rightarrow BD=a\Rightarrow \Delta ABD$ là tam giác đều cạnh bằng a

$\large SA=SB=SD$, suy ra hình chiếu H của S lên mặt đáy là trọng tâm tam giác ABD

$\large AH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}$. Góc giữa SA và mặt đáy là góc $\large SAH=45^\circ\Rightarrow SH=AH=\dfrac{a\sqrt{3}}{3}$

Thể tích khối chóp S. ABC bằng $\large V=\dfrac{1}{3}.SH.S_{ABC}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{3}.\dfrac{1}{2}.a.a\sqrt{3}=\dfrac{a^3}{6}$