Cho hàm số $\large f(x)=ax^3+bx^2+cx+d$ có đồ thị như hình vẽ bên. Hỏi

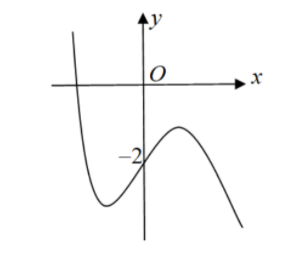
Cho hàm số $\large f(x)=ax^3+bx^2+cx+d$ có đồ thị như hình vẽ bên. Hỏi phương trình $\large [f(x)]^2=4$ có bao nhiêu nghiệm?

 

• A. A. 5
• B. B. 6
• C. C. 3
• D. D. 4

Chọn D

Ta có: $\large [f(x)]^2=4\Leftrightarrow $ $\large \left[\begin{align}& f(x)=2\\& f(x)=-2\\\end{align}\right. $

Từ đồ thị hàm số f(x) ta có đồ thị hàm số f(x) cắt đường thẳng $\large y=2$ tại một điểm và cắt đường thẳng $\large y=-2$ tại ba điểm phân biệt (hoành độ các giao điểm khác nhau) nên phương trình $\large f(x)=2$ có một nghiệm và phương trình $\large f(x)=-2$ có ba nghiệm

Vậy phương trình $\large [f(x)]^2=4$ có 4 nghiệm