Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bầng, cạnh bên bằn

Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bầng, cạnh bên bằng $\large a\sqrt{3}$. Gọi O là tâm của đáy ABC, $\large d_1$ là khoảng cách từ A đến mặt phẳng (SBC) và $\large d_2$ là khoảng cách từ O đến mặt phẳng (SBC). Tính $\large d= d_1+d_2$

• A. A. $\large d= \dfrac{2a\sqrt{15}}{11}$
• B. B. $\large d= \dfrac{2a\sqrt{2}}{33}$
• C. C. $\large d= \dfrac{8a\sqrt{2}}{33}$
• D. D. $\large d= \dfrac{8a\sqrt{2}}{11}$

Chọn C

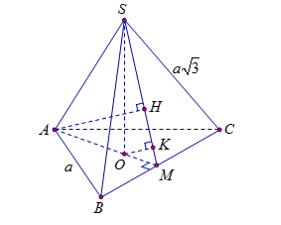
Do tam giác ABC đều tâm O suy ta $\large AO\perp BC$ tại M là trung điểm của BC
Ta có: $\large AM=\dfrac{a\sqrt{3}}{2},\, MO=\dfrac{1}{3}AM=\dfrac{a\sqrt{3}}{6},\, OA= \dfrac{2}{3}AM=\dfrac{a\sqrt{3}}{3}$
Từ giả thiết hình chóp đều suy ra $\large SO\perp (ABC)$
$\large SO=\sqrt{SA^2-OA^2}=\sqrt{3a^2-\dfrac{3a^2}{9}}= \dfrac{2a\sqrt{6}}{3}$
Dựng $\large OK\perp SM,\, AH\perp SM\Rightarrow  AH// OK;\, \dfrac{OK}{AH}= \dfrac{OM}{AM}=\dfrac{1}{3}$
Có $\large \left\{\begin{align}& BC\perp  SO\\&BC\perp AM \\\end{align} \right.$ $\large \Rightarrow  BC\perp (SAM)\Rightarrow  BC\perp OK$
Có $\large \left\{\begin{align}& OK\perp SM\\& OK\perp BC\\\end{align} \right.$ $\large \Rightarrow  OK\perp (SBC),\, AH\perp (SBC)$ (do $\large AH// OK$)
Từ đó: $\large d_1= d(A, (SBC))= AH= 3OK;\, d_2= d(O, (SBC))= OK$
Trong tam giác vuôgn OSM có đường cao OK nên 
$\large \dfrac{1}{OK^2}= \dfrac{1}{OM^2}+\dfrac{1}{SO^2}= \dfrac{36}{3a^2}+\dfrac{9}{24a^2}=\dfrac{99}{8a^2}\Rightarrow  OK= \dfrac{2a\sqrt{2}}{33}$
Vậy: $\large d= d_1+d_2= 4OK= \dfrac{8a\sqrt{2}}{33}$