Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, $\Large AB=3a,

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, $\Large AB=3a, BC=4a$. Cạnh bên SA vuông góc với đáy. Góc tạo bởi SC và đáy bằng $\Large 60^{\circ}$. Gọi M là trung điểm của AC, tính khoảng cách giữa hai đường thẳng AB và SM.
Đáp án án đúng là: B
Lời giải chi tiết:
Chọn B
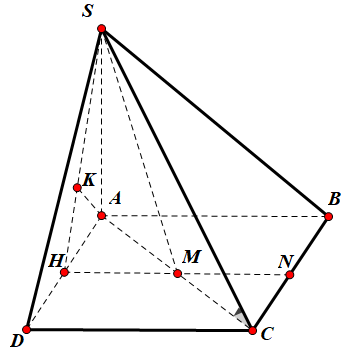
Ta có: $\Large \left ( SC,(ABC) \right )=\widehat{SCA}=60^{0}\Rightarrow AC=5a, SA=5a\sqrt{3}$.
Gọi N là trung điểm BC $\Large \Rightarrow AB // (SMN) \Rightarrow d(AB, SM)=d\big(A, (SMN)\big)$.
Dựng $\Large AH\perp MN$ tại H trong (ABC).
Dựng $\Large AK \perp SH$ tại K trong (SAH).
$\Large \Rightarrow AK \perp (SMN)$ tại K nên $\Large d\big(A, (SMN)\big)=AK \Rightarrow d[AB, SM]=AK$.
$\Large AH=NB=2a$.
$\Large \dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}=\dfrac{1}{4a^2}+\dfrac{1}{75a^2}=\dfrac{79}{300a^2} \Rightarrow AK=\dfrac{10a\sqrt{3}}{\sqrt{79}}$.
Xem thêm các bài tiếp theo bên dưới
- Cho hàm số $\Large f(x)=\dfrac{1}{3}x^3+2x^2+(m+1)x+5$. Tìm tất cả các
- Có một cốc thủy tinh hình trụ, bán kính trong lòng đáy cốc là 4 cm, ch
- Trong không gian $\Large Oxyz$, cho đường thẳng $\Large d: \dfrac{x-1}
- Một hình trụ có bán kính đáy bằng 5 và khoảng cách giữa hai đáy bằng 7
- Xét hàm số $\Large f(x)$ liên tục trên đoạn [0; 1] và thỏa mãn $\Large