Cho hình chóp S.ABCD có SA=x(0<x<√3), tất c
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có SA=x(0<x<√3), tất cả các cạnh còn lại bằng nhau và bằng 1. Với giá trị nào của x thì thể tích khối chóp đã cho lớn nhất.
Đáp án án đúng là: C
Lời giải chi tiết:
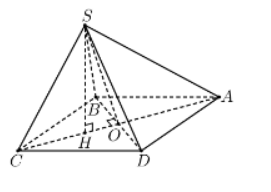
Gọi O là tâm của hình thoi ABCD→OA=OC(1)
Theo bài ra, ta có △SBD=△CBD⇒OS=OC
Từ (1) và (2) ta có OS=OA=OC=12AC⇒△SAC vuông tại S⇒AC=√x2+1
Suy ra OA=√x2+12 và OB=√AB2−OA2=√3−x22
Ta có SB=SC=SD=1, suy ra hình chiếu vuông góc H của đỉnh S trên mặt đáy là tâm đường tròn ngoại tiếp tam giác BCD⟶H∈AC
Trong tam giác vuông SAC, ta có SH=SA.SC√SA2+SC2=x√x2+1
Khi đó VS.ABCD=13SABCD.SH=13⋅√(x2+1)(3−x2)2⋅x√x2+1=16x√3−x2≤16⋅(x2+3−x22)=14
Dấu "=" xảy ra ⇔x=√3−x2⇔x=√62
Đáp án C
Xem thêm các bài tiếp theo bên dưới
- Cho tam giác OAB đều cạnh a. Trên đường thẳng $\larg
- Một hộp không nắp được làm từ một mảnh cactong theo hình vẽ. Hộp có đá
- Để thiết kế một chiếc bể cá hình chữ nhật không nắp có chiều cao là 60
- Cho hình hộp ABCD.A′B′C′D′ có đáy ABCD là hình thoi
- Một viên đá dạng khối chóp tứ diện đều và tất cả các cạnh đều bằng $\l