Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình vuông cạnh
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình vuông cạnh $\Large a, SA\perp (ABCD)$ và $\Large SA=a\sqrt{6}$. Gọi $\Large \alpha$ là góc giữa $\Large SC$ và $\Large (SAB)$. Giá trị $\Large \alpha$ bằng
Đáp án án đúng là: B
Lời giải chi tiết:
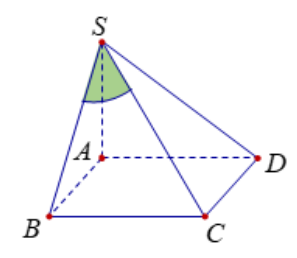
$\Large \alpha=[\widehat{SC,(SAB)}]=\widehat{CSB}$
$\Large SB=\sqrt{SA^{2}+AB^{2}}=\sqrt{(a\sqrt{6})^{2}+a^{2}}=a\sqrt{7}$
Tam giác SBC vuông tại B nên $\Large \tan \alpha=\dfrac{BC}{SB}=\dfrac{a}{a\sqrt{7}}=\dfrac{\sqrt{7}}{7}$
Xem thêm các bài tiếp theo bên dưới
- Tổng số các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $\
- Trong không gian Oxyz, cho mặt cầu $\Large (S): x^{2}+y^{2}+z^{2}+2x+4
- Cho hàm số $\Large y=f(x)$ có đồ thị như hình vẽ dưới đây. Tìm tất cả
- Khi cắt khối trụ (T) bởi một mặt phẳng qua trục của nó ta được thiết d
- Nghiệm của bất phương trình $\Large \left(\dfrac{1}{5}\right)^{9x^{2}-