Cho hình chóp S.ABCD có đáy ABCD là hình bình hành,
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, trên cạnh SA lấy điểm M và đặt SMSA=x. Giá trị x để mặt phẳng (MBC) chia khối chóp đã cho thành hai phần có thể tích bằng nhau là
Đáp án án đúng là: B
Lời giải chi tiết:
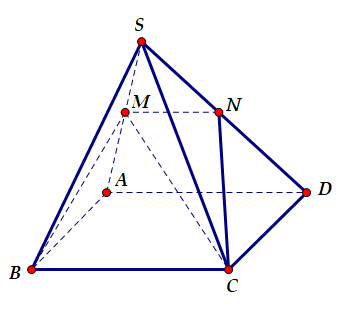
Ta có:
{BC//(SAD)BC⊂(BMC) ⇒(SAD)∩(BMC)=MN//BC⇒SMSA=SNSD=x
VS.MBCVS.ABC=2VS.MBCV=SMSA=x
VS.MCNVS.ACD=2VS.MCNV=SMSA.SNSD=x2
⇒2(VS.MCN+VS.MBC)V=x+x2⇔2VS.MBCNV=x+x2⇔VS.MBCNV=x+x22 (1)
Mặt phẳng (MBC) chia khối chóp đã cho thành hai phần có thể tích bằng nhau VS.MBCNV=12 (2)
Từ (1) và (2) ta có: 1=x+x2⇔x=√5−12
Đáp án B
Xem thêm các bài tiếp theo bên dưới