Cho lăng trụ ABC.A′B′C′ có thể tích bằng 2. Gọi M,N
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho lăng trụ ABC.A′B′C′ có thể tích bằng 2. Gọi M,N lần lượt là hai điểm nằm trên hai cạnh AA′ và BB′ sao cho M là trung điểm của AA′ và BN=23BB′. Đường thẳng CM cắt đường thẳng C′A′ tại P và đường thẳng CN cắt đường thẳng C′B′ tại Q, Thể tích khối đa diện A′MPB′NQ bằng
Đáp án án đúng là: C
Lời giải chi tiết:
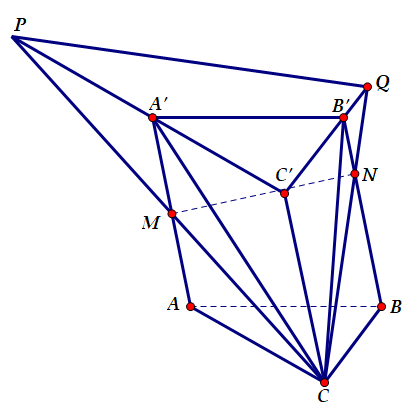
Ta có: QB′QC′=B′NC′C=B′NB′B=13⇒QC′B′C′=32
S△PQC′S△A′B′C′=PC′A′C′.QC′B′C′=2.32=3⇒S△PQC′=3S△A′B′C′
Đặt h=d(C;(A′B′C′))
VC.ABB′A′=23S△PQC.h=13.3S△A′B′C′h=S△A′B′C′.h=VABC.A′B′C′=2
Mặt khác VC.ABB′A′=23VABC.A′B′C′=43
VC.ABNMVC.ABB′A′=SABNMSABB′A′=AM+BNAA′+BB′=12AA′+23AA′AA′+AA′=712⇒VC.ABNM=712.VC.ABB′A′=712VC.ABB′A′=712.43=79
Suy ra: VCC′MNB′A′=VABC.A′B′C′−VC.ABNM=2−79=19
Vậy: VA′MPB′NQ=VC.PQC′−VCC′MNB′A′=2−119=79
Đáp án C
Xem thêm các bài tiếp theo bên dưới
- CHo hình chóp S.ABC có đáy ABC là tam giác đều và có
- Cho hình chóp S.ABCD có đáy là hình chữ nhật với $\large AB=4
- Cho hình chóp S.ABC có đáy là tam giác vuông cân tại $\large
- Cho một tấm bìa hình chữ nhật có kích thước 60cmx40cm. Người ta cắt 6
- Người ta cắt một tờ giấy hình vuông cạnh bằng 1 để gấp thành một hình