Cho hình chóp $\large S.ABCD$ có đáy $\large ABCD$ là hình bình hành.

Cho hình chóp $\large S.ABCD$ có đáy $\large ABCD$ là hình bình hành. Gọi $\large M,N$ lần lượt là trung điểm của các cạnh $\large AB,BC$. Điểm $\large I$ thuộc đoạn $\large SA$. Biết mặt phẳng $\large (MNI)$ chia khối chóp $\large S.ABCD$ thành hai phần, phần chứa đỉnh $\large S$ có thể tích bằng $\large\dfrac{7}{13}$ lần phần còn lại. Tính tỉ số $\large k=\dfrac{IA}{IS}$

• A.

  A. $\large\dfrac{1}{2}$

• B.

  B. $\large\dfrac{2}{3}$

• C.

  C. $\large\dfrac{1}{3}$

• D.

  D. $\large\dfrac{3}{4}$

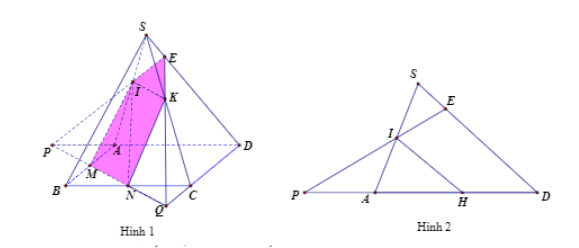
Mặt phẳng chứa $\large (MNI)$ cắt khối chóp theo thiết diện như hình 1. Đặt $\large V_{S.ABCD}=V$

Ta có $\large S_{\bigtriangleup APM}=S_{\bigtriangleup BMN}=\dfrac{1}{4}S_{\bigtriangleup ABC}=\dfrac{1}{8}S_{ABCD}\Rightarrow \dfrac{S_{\bigtriangleup APM}}{S_{ABCD}}=\dfrac{1}{8}$

$\large\dfrac{d(I,(ABCD))}{d(S,(ABCD))}=\dfrac{IA}{SA}=\dfrac{k}{k+1}$

$\large\Rightarrow \dfrac{V_{I.APM}}{V_{S.ABCD}}=\dfrac{S_{\bigtriangleup APM}}{S_{ABCD}}\cdot \dfrac{d(I,(ABCD))}{d(S.(ABCD))}=\dfrac{k}{8(k+1)}\Rightarrow V_{I.APM}=\dfrac{k}{8(k+1)}V$

Do $\large MN//AC\Rightarrow IK//AC\Rightarrow IK//(ABCD)\Rightarrow d(I;(ABCD))=d(K;(ABCD))$

Mà $\large S_{\bigtriangleup APM}=S_{\bigtriangleup NCQ}\Rightarrow V_{I.APM}=V_{K.NCQ}=\dfrac{k}{8(k+1)}V$

Kẻ $\large IH//SD(H\in AD)$ như hình 2, ta có:

$\large\dfrac{IH}{SD}=\dfrac{AH}{AD}=\dfrac{AI}{AS}=\dfrac{k}{k+1}$

$\large \dfrac{IH}{ED}=\dfrac{PH}{PD}=\dfrac{PA}{PD}+\dfrac{AH}{PD}=\dfrac{PA}{PD}+\dfrac{2AH}{3AD}=\dfrac{1}{3}+\dfrac{2k}{3(k+1)}=\dfrac{3k+1}{3(k+1)}$

$\large \Rightarrow \dfrac{ED}{SD}=\dfrac{IH}{SD}:\dfrac{ID}{ED}=\dfrac{3k}{3k+1}\Rightarrow \dfrac{d(E,(ABCD))}{d(S,(ABCD))}=\dfrac{ED}{SD}=\dfrac{3k}{3k+1}$

$\large \dfrac{S_{\Delta PQD}}{S_{\Delta ABCD}}=\dfrac{9}{8}\Rightarrow \dfrac{V_{E.PQD}}{V_{S.ABCD}}=\dfrac{27k}{24k+8}\Rightarrow V_{E.PQD}=\dfrac{27k}{24k+8}.V$

$\large V_{EIKAMNCD}=\dfrac{13}{20}V\Leftrightarrow V_{E.PDC}-V_{I.APM}-V_{K.NQC}=\dfrac{13}{20}V$

$\large\Leftrightarrow \dfrac{27k}{8(3k+1)}V-\dfrac{k}{8(k+1)}V-\dfrac{k}{8(k+1)}V=\dfrac{13}{20}V$

$\large\Leftrightarrow \dfrac{27k}{2(3k+1)}-\dfrac{k}{k+1}=\dfrac{13}{5}\Leftrightarrow k=\dfrac{2}{3}$

Đáp án B