Cho hình chóp tứ giác đều $\large S.ABCD$ đỉnh $\large S$, khoảng cách

Cho hình chóp tứ giác đều $\large S.ABCD$ đỉnh $\large S$, khoảng cách từ điểm $\large C$ đến mặt phẳng $\large (SAB)$ bằng 6. Gọi $\large V$ là thể tích khối chóp $\large S.ABCD$, tính giá trị nhỏ nhất của $\large V$

• A.

  A. $\large 18\sqrt{3}$

• B.

  B. $\large 54\sqrt{3}$

• C.

  C. $\large 64\sqrt{3}$

• D.

  D. $\large 27\sqrt{3}$

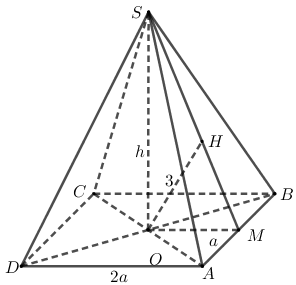
Gọi $\large O$ là giao điểm của $\large AC$ và $\large BD, M$ là trung điểm $\large AB$.

Vì $\large S.ABCD$ là hình chóp tứ giác đều nên $\large SO\perp (ABCD)$.

Ngoài ra $\large CO$ cắt $\large (SAB)$ tại $\large A$ nên $\large\dfrac{d(O;(SAB))}{d;(C;(SAB))}=\dfrac{AO}{AC}=\dfrac{1}{2}$

$\large\Rightarrow d(O;(SAB))=\dfrac{1}{2}.d(C;(SAB))=\dfrac{6}{2}=3$

Ta có: $\large\left\{\begin{align}AB\perp SO(SO\perp (ABCD))\\ AB\perp OM(OM//AD)\end{align}\right.$ $\large\Rightarrow AB\perp (SOM)$

$\large\Rightarrow (SAB)\perp (SOM)$

mà $\large (SAB)\cap (SOM)=SM$ trong $\large (SOM)$, kẻ $\large OH\perp SM$ tại $\large H$

Suy ra $\large OH\bot \left( SAB \right)\Rightarrow OH=d\left( O;\left( SAB \right) \right)=3$

Đặt $\large AD=2a,SO=h(a,h>0)$.

Áp dụng hệ thức lượng trong $\large\bigtriangleup SOM$ vuông tại $\large O$ có $\large SO=h,OM=a,OH=3$, ta được:

$\large\dfrac{1}{OH^{2}}=\dfrac{1}{SO^{2}}+\dfrac{1}{OM^{2}}\Rightarrow \dfrac{1}{h^{2}}+\dfrac{1}{a^{2}}=\dfrac{1}{9}$

Mà $\large V=V_{S.ABCD}=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{h.(2a)^{2}}{3}=\dfrac{4}{3}a^{2}h\Rightarrow a^{2}h=\dfrac{3}{4}V$

Áp dụng BĐT Cauchy cho 3 số dương $\large\dfrac{1}{h^{2}},\dfrac{1}{2a^{2}},\dfrac{1}{2a^{2}}$, ta được:

$\large\dfrac{1}{h^{2}}+\dfrac{1}{2a^{2}}+\dfrac{1}{2a^{2}}\geq 3\sqrt[3]{\dfrac{1}{h^{2}}\cdot \dfrac{1}{2a^{2}}\cdot\dfrac{1}{2a^{2}}}$

$\large\Rightarrow \dfrac{1}{9}\geq \dfrac{3}{\sqrt[3]{4a^{4}h^{2}}}\Rightarrow \sqrt[3]{4a^{4}h^{2}}\geq 27\Rightarrow  4(a^{2}h)^{2}\geq 27^{3}$

$\large\Rightarrow a^{2}h\geq \sqrt{\dfrac{27^{3}}{4}}\Rightarrow \dfrac{3}{4}V\geq \dfrac{81\sqrt{3}}{2}\Rightarrow V\geq 54\sqrt{3}$

$\large V=54\sqrt{3}\Leftrightarrow \left\{\begin{align}\dfrac{1}{h^{2}}+\dfrac{1}{a^{2}}=\dfrac{1}{9}\\ \dfrac{1}{h^{2}}=\dfrac{1}{2a^{2}}\end{align}\right.$ $\large\Leftrightarrow \left\{\begin{align}\dfrac{1}{h^{2}}=\dfrac{1}{27}\\ \dfrac{1}{a^{2}}=\dfrac{2}{27}\end{align}\right.$ $\large\Leftrightarrow \left\{\begin{align}h=3\sqrt{3}\\ a=\dfrac{3\sqrt{6}}{2}\end{align}\right.$

Vậy $\large V_{min}=54\sqrt{3}$

Đáp án B