Cho hình chóp $\Large S.ABCD$ có đáy là hình vuông, mặt bên $\Large (S

MỤC LỤC
Câu hỏi:
Cho hình chóp $\Large S.ABCD$ có đáy là hình vuông, mặt bên $\Large (SAB)$ là một tam giác đều nằm trong mặt phẳng vuông góc với mặt đáy $\Large (ABCD)$ và có diện tích bằng $\Large \dfrac{27\sqrt{3}}{4}$ (đvdt). Một mặt phẳng đi qua trọng tâm tam giác $\Large SAB$ và song song với mặt đáy $\Large (ABCD)$ chia khối chóp $\Large S.ABCD$ thành hai phần, tính thể tích $\Large V$ của phần chứa điểm $\Large S$.
Đáp án án đúng là: D
Lời giải chi tiết:
Chọn D
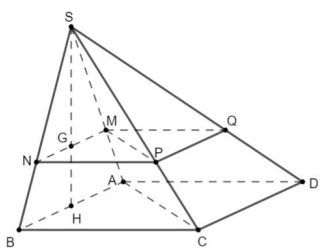
Gọi $\Large H$ là trung điểm của $\Large AB.$
Do $\Large \Delta SAB$ đều và $\Large (SAB) \bot (ABCD)$ nên $\Large SH \bot (ABCD).$
Ta có:
$\Large S_{\Delta ABC} = \dfrac{AB^{2}\sqrt{3}}{4} = \dfrac{27\sqrt{3}}{4}$
$\Large \Rightarrow AB = 3\sqrt{3}$
$\Large \Rightarrow SH = \dfrac{AB\sqrt{3}}{2} = \dfrac{3\sqrt{3}.\sqrt{3}}{2} = \dfrac{9}{2}$
$\Large \Rightarrow V_{S.ABCD} = \dfrac{1}{3}. S_{ABCD}.SH = \dfrac{1}{3}. AB^{2}.SH$ $\Large = \dfrac{1}{3} (3\sqrt{3})^{2}.\dfrac{9}{2}$ $\Large = \dfrac{81}{2}$ (đvtt).
Gọi $\Large G$ là trọng tâm tam giác $\Large SAB,$ qua $\Large G$ kẻ đường thẳng song song với $\Large AB,$ cắt $\Large SA$ và $\Large SB$ lần lượt tại $\Large M$ và $\Large N.$ Qua $\Large N$ kẻ đường thẳng song song với $\Large BC$ cắt $\Large SC$ tại $\Large P,$ qua $\Large M$ kẻ đường thẳng song song với $\Large AD$ cắt $\Large SD$ tại $\Large Q.$ Suy ra $\Large (MNPQ)$ là mặt phẳng đi qua $\Large G$ và song song với $\Large (ABCD).$
Khi đó:
$\Large \dfrac{SM}{SA} = \dfrac{SN}{SB} = \dfrac{SP}{SC} = \dfrac{SQ}{SD} = \dfrac{SG}{SH} = \dfrac{2}{3}.$
Có $\Large \dfrac{V_{S.MNP}}{V_{S.ABC}} = \dfrac{SM}{SA} .\dfrac{SN}{SB} . \dfrac{SP}{SC} = \left ( \dfrac{2}{3} \right )^{3} = \dfrac{8}{27}$
$\Large \Rightarrow V_{S.MNP} = \dfrac{8}{27}. V_{S.ABC} = \dfrac{8}{27}. \dfrac{1}{2} . V_{S.ABCD}$ $\Large = \dfrac{4}{27} . V_{S.ABCD}.$
Có $\Large \dfrac{V_{S.MPQ}}{V_{S.ACD}} = \dfrac{SM}{SA} .\dfrac{SP}{SC} . \dfrac{SQ}{SD} = \left ( \dfrac{2}{3} \right )^{3} = \dfrac{8}{27}$
$\Large \Rightarrow V_{S.MPQ} = \dfrac{8}{27}. V_{S.ACD} = \dfrac{8}{27}. \dfrac{1}{2} . V_{S.ABCD}$ $\Large = \dfrac{4}{27} . V_{S.ABCD}.$
Vậy $\Large V_{S.MNPQ} = V_{S.MNP} + V_{S.MPQ}$
$\Large = \dfrac{4}{27} . V_{S.ABCD} + \dfrac{4}{27} . V_{S.ABCD}$
$\Large = \dfrac{8}{27} . V_{S.ABCD}$
$\Large = \dfrac{8}{27}.\dfrac{81}{2}$
$\Large = 12$ (đvtt).
Xem thêm các bài tiếp theo bên dưới
- Trong mặt phẳng tọa độ $\Large Oxy$, tập hợp điểm biểu diễn các số phứ
- Cho $\Large a$ là số thực dương. Tính $\Large I = \int_{0}^{a}\sin^{20
- Số hạng không chứa $\Large x$ trong khai triển $\Large \left ( \sqrt[3
- Tính tổng tất cả các nghiệm của phương trình $\Large e^{\sin\left(x-\d
- Trong tất cả các hình nón nội tiếp trong hình cầu có thể tích bằng $\L